Question

【题目】已知函数f（x）是定义在（0，+∞）上的单调增函数，满足f（xy）=f（x）+f（y），f（3）=1
（1）求f（1）、f（ ）的值；
（2）若满足f（x）+f（x﹣8）≤2，求x的取值范围．

Answer 1

【答案】
（1）解：令x=y=1得：f（11）=f（1）+f（1），

∴f（1）=0；

令y= ，则f（x ）=f（x）+f（ ）=f（1）=0，

∵f（3）=1，

∴f（ ）=﹣f（3）=﹣1

（2）解：∵f（9）=f（3）+f（3）=2，

∴f（x）+f（x﹣8）≤2f[x（x﹣8）]≤f（9），

而函数f（x）在定义域（0，+∞）上为增函数，

∴ ，

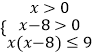解得：8＜x≤9，

∴x的取值范围是（8，9]

【解析】（1）令x=y=1易得f（1）=0；令y= ，可得f（x）+f（ ）=0，于是由f（3）=1可求得f（ ）的值；（2）由f（x）+f（x﹣8）＜2，知f（x）+f（x﹣8）=f[x（x﹣8）]＜f（9），再由函数f（x）在定义域（0，+∞）上为增函数，能求出原不等式的解集．