题目内容
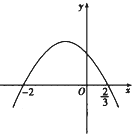
【题目】已知命题p:lg(x2-2x-2)≥0;命题q:0<x<4.若p且q为假,p或q为真,求实数x的取值范围.
【答案】【解答】由lg(x2-2x-2)≥0,得x2-2x-2≥1,
∴x≥3,或x≤-1.即p:x≥3,或x≤-1.
∴ ![]() p:-1<x<3.又∵q:0<x<4,
p:-1<x<3.又∵q:0<x<4,
∴ ![]() q:x≥4,或x≤0.
q:x≥4,或x≤0.
由p且q为假,p或q为真知p , q一真一假,
当p真q假时,由  得x≥4,或x≤-1,
得x≥4,或x≤-1,
当p假q真时,由![]() 得0<x<3,
得0<x<3,
∴实数x的取值范围是{x|x≤-1,或0<x<3,或x≥4},
故{x|x≤-1,或0<x<3,或x≥4}
【解析】根据p且q为假,p或q为真,作出判断,由判断复合命题的口诀(或命题:有真则真;且命题:有假则假;非命题:真假相反。)

练习册系列答案
相关题目
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图象
在某一个周期内的图象
时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 5 |
| 0 |
(Ⅰ)请将上表数据补充完整,填写在答题卡上相应位置,并直接写出函数![]() 的解
的解
析式;
(Ⅱ)将![]() 图象上所有点向左平行移动
图象上所有点向左平行移动![]()
![]() 个单位长度,得到
个单位长度,得到![]() 的图
的图
象. 若![]() 图象的一个对称中心为
图象的一个对称中心为![]() ,求
,求![]() 的最小值.
的最小值.