题目内容
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M: ![]() 及其上一点A(2,4)
及其上一点A(2,4)
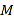
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B、C两点,且BC=OA,求直线l的方程;
(3)设点T(t,o)满足:存在圆M上的两点P和Q,使得![]() ,求实数t的取值范围。
,求实数t的取值范围。
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)根据直线与x轴相切确定圆心位置,再根据两圆外切建立等量关系求半径;(2)根据垂径定理确定等量关系,求直线方程;(3)利用向量加法几何意义建立等量关系,根据圆中弦长范围建立不等式,求解即得参数取值范围.
试题解析:解:圆M的标准方程为![]() ,所以圆心M(6,7),半径为5,.
,所以圆心M(6,7),半径为5,.
(1)由圆心N在直线x=6上,可设![]() .因为N与x轴相切,与圆M外切,
.因为N与x轴相切,与圆M外切,
所以![]() ,于是圆N的半径为
,于是圆N的半径为![]() ,从而
,从而![]() ,解得
,解得![]() .
.
因此,圆N的标准方程为![]() .
.
(2)因为直线l∥OA,所以直线l的斜率为![]() .
.
设直线l的方程为y=2x+m,即2x-y+m=0,
则圆心M到直线l的距离
![]()
因为![]()
而![]()
所以![]() ,解得m=5或m=-15.
,解得m=5或m=-15.
故直线l的方程为2x-y+5=0或2x-y-15=0.
(3)设![]()
因为![]() ,所以
,所以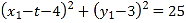 ……①
……①
因为点Q在圆M上,所以![]() …….②
…….②
将①代入②,得![]() .
.
于是点![]() 既在圆M上,又在圆
既在圆M上,又在圆![]() 上,
上,
从而圆![]() 与圆
与圆![]() 没有公共点,
没有公共点,
所以![]() 解得
解得![]() .
.
因此,实数t的取值范围是![]() .
.

练习册系列答案
相关题目
