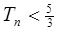题目内容
数列 的前
的前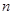 项和记为
项和记为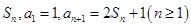
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)等差数列 的各项为正,其前
的各项为正,其前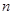 项和为
项和为 ,且
,且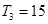 ,又
,又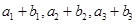 成等比数列,求
成等比数列,求
(Ⅰ)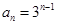 (Ⅱ)
(Ⅱ)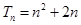
解析试题分析:(Ⅰ)由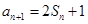 可得
可得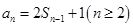 ,两式相减得
,两式相减得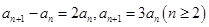 3分
3分
又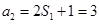 ∴
∴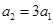
故 是首项为
是首项为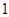 ,公比为
,公比为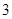 得等比数列
得等比数列
∴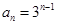 6分
6分
(Ⅱ)设 的公差为
的公差为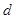
由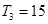 得,可得
得,可得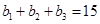 ,可得
,可得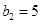
故可设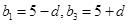
又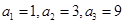
由题意可得
解得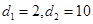
∵等差数列 的各项为正,∴
的各项为正,∴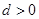
∴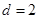 10分
10分
∴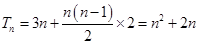 12分
12分
考点:等差数列等比数列性质及由数列前n项和求通项
点评:由前n项和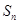 求通项
求通项 时需分情况讨论:
时需分情况讨论: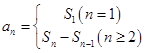 ,最终看其结果能否合并为一个关系式
,最终看其结果能否合并为一个关系式

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
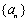 前三项的和为
前三项的和为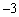 ,前三项的积为
,前三项的积为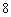 .
.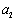 ,
,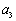 ,
,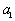 成等比数列,求数列
成等比数列,求数列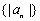 的前
的前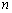 项和.
项和.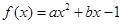 ,且不等式
,且不等式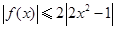 对任意的实数
对任意的实数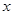 恒成立,数列
恒成立,数列 满足
满足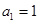 ,
,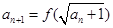
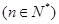 .
. 的值;
的值; .
.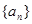 的前
的前 项和为
项和为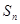 ,且满足
,且满足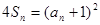 (
(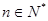 ).
).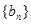 的通项公式为
的通项公式为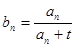 (
(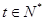 ),若
),若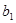 ,
,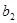 ,
,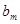 (
(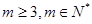 )成等差数列,求
)成等差数列,求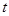 和
和 的值;
的值;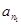 ,
,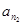 ,
,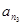 .
.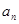 }中,a1=3,
}中,a1=3,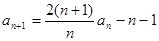 ,
,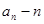 关于n的表达式(不用证明);
关于n的表达式(不用证明);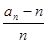 }是什么类型的数列并证明;
}是什么类型的数列并证明; 满足
满足 .
. 是等差数列;
是等差数列; ,求数列
,求数列 的前
的前 项和
项和 .
. }的前n项和为
}的前n项和为 ,且
,且 =1,
=1,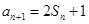 ,数列{
,数列{ }满足
}满足 ,点P(
,点P( )在直线x―y+2=0上,
)在直线x―y+2=0上, .
. ,求数列{
,求数列{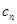 }的前n项和
}的前n项和 .
.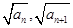 )在双曲线y2-x2=1上,点(
)在双曲线y2-x2=1上,点(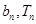 )在直线y=-
)在直线y=-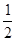 x+1上,其中Tn是数列{bn}的前n项和。
x+1上,其中Tn是数列{bn}的前n项和。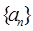 中,
中,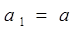 ,
, 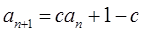
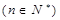
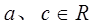
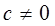
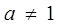 时,
时, 是等比数列,并求
是等比数列,并求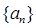 通项公式。
通项公式。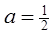 ,
,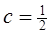 ,
,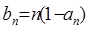
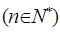 求:数列
求:数列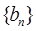 的前n项的和
的前n项的和 。
。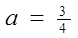 、
、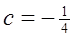 、
、 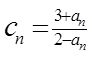 。记
。记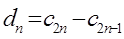 ,数列
,数列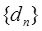 的前n项和
的前n项和 。证明:
。证明: