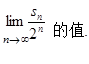题目内容
(本题满分12分)已知数列 满足
满足 .
.
(Ⅰ)证明数列 是等差数列;
是等差数列;
(Ⅱ)求数列 的通项公式;
的通项公式;
(Ⅲ)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
解析试题分析:
解:(Ⅰ)由已知可得 ,所以
,所以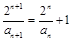 ,即
,即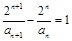 ,
,
∴数列 是公差为1的等差数列. 4分
是公差为1的等差数列. 4分
(Ⅱ)由(Ⅰ)可得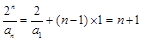 ,∴
,∴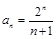 . . 7分
. . 7分
(Ⅲ)由(Ⅱ)知,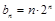 ,
,
所以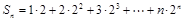 ,
,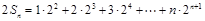 ,
,
相减得
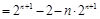 ,
,
∴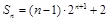 . . . . . 12分
. . . . . 12分
考点:本题考查等差数列与等比数列的概念与通项公式、数列求和等基础知识知识,考查运算求解能力、推理论证能力,中等题.
点评:

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 的前项和为
的前项和为 ,满足
,满足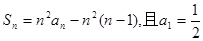 ,
,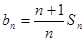 ,证明:
,证明: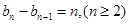 ;
; ,求n的值;
,求n的值; 的数学公式表示上述结论,并给予证明。
的数学公式表示上述结论,并给予证明。
 的前
的前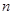 项和记为
项和记为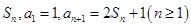
 的各项为正,其前
的各项为正,其前 ,且
,且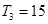 ,又
,又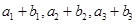 成等比数列,求
成等比数列,求 的前
的前 项和为
项和为 ,满足
,满足 .
.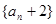 为等比数列;
为等比数列; 满足
满足 ,
, 为数列
为数列 的前
的前 .
.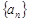 的前 n项和为
的前 n项和为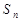 ,满足
,满足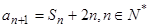 ,且
,且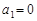 .
. ,
, ;
;  ,求证:数列
,求证:数列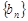 是等比数列。
是等比数列。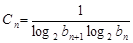 , 求数列
, 求数列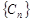 的前n项和
的前n项和 。
。 中,
中,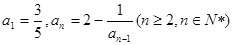 ,数列
,数列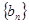 满足
满足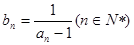 。
。 中,已知
中,已知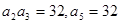 .
. 求数列
求数列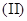 设数列
设数列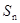 ,求
,求