题目内容
【题目】在公差为d的等差数列{an}中,已知a1=10,且a1 , 2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
【答案】
(1)解:由题意得 ![]() ,即
,即 ![]() ,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.
,整理得d2﹣3d﹣4=0.解得d=﹣1或d=4.
当d=﹣1时,an=a1+(n﹣1)d=10﹣(n﹣1)=﹣n+11.
当d=4时,an=a1+(n﹣1)d=10+4(n﹣1)=4n+6.
所以an=﹣n+11或an=4n+6;
(2)解:设数列{an}的前n项和为Sn,因为d<0,由(Ⅰ)得d=﹣1,an=﹣n+11.
则当n≤11时, ![]() .
.
当n≥12时,|a1|+|a2|+|a3|+…+|an|=﹣Sn+2S11= ![]() .
.
综上所述,
|a1|+|a2|+|a3|+…+|an|= 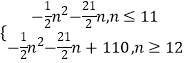 .
.
【解析】(1)直接由已知条件a1=10,且a1 , 2a2+2,5a3成等比数列列式求出公差,则通项公式an可求;(2)利用(1)中的结论,得到等差数列{an}的前11项大于等于0,后面的项小于0,所以分类讨论求d<0时|a1|+|a2|+|a3|+…+|an|的和.
【考点精析】掌握等差数列的通项公式(及其变式)和数列的前n项和是解答本题的根本,需要知道通项公式:![]() 或
或![]() ;数列{an}的前n项和sn与通项an的关系
;数列{an}的前n项和sn与通项an的关系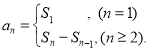 .
.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目