题目内容
(本小题满分12分)已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 。
。
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: 。
。
 的前
的前 项和为
项和为 ,且满足
,且满足 。
。(Ⅰ)求数列
 的通项公式;
的通项公式;(Ⅱ)设
 ,数列
,数列 的前
的前 项和为
项和为 ,求证:
,求证: 。
。(Ⅰ)
 .
.
(Ⅱ) ,所以
,所以
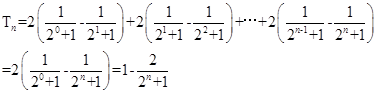
所以 。
。

 .
.(Ⅱ)
 ,所以
,所以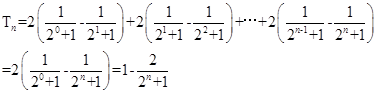
所以
 。
。 试题分析:(Ⅰ)当
 时,
时,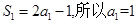 ;
;当
 时,
时, ,所以数列
,所以数列 是首项为1,公比为2的等比数列。所以
是首项为1,公比为2的等比数列。所以
 .
.(Ⅱ)由(Ⅰ)知
 ,所以
,所以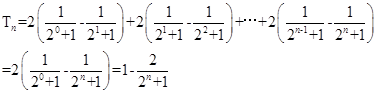
所以
 。
。 ,
,点评:我们要熟练掌握求数列通项公式的方法。公式法是求数列通项公式的基本方法之一,常用的公式有:等差数列的通项公式、等比数列的通项公式及公式
 。此题的第一问求数列的通项公式就是用公式
。此题的第一问求数列的通项公式就是用公式 ,用此公式要注意讨论
,用此公式要注意讨论 的情况。
的情况。
练习册系列答案
相关题目
 是等差数列,且
是等差数列,且 ,则这个数列的前5项和
,则这个数列的前5项和 =
=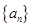 的各项均为正数,且满足
的各项均为正数,且满足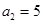 ,
,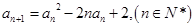 .
. 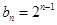 ,令
,令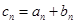 ,求数列
,求数列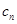 的前
的前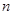 项和
项和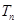
 满足
满足
 ; (Ⅱ)证明
; (Ⅱ)证明 .
.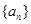 的前n项和
的前n项和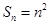 ,则
,则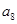 的值为( )
的值为( ) 中,
中, ,
, ,记
,记 为
为 项的和,则
项的和,则 = ;
= ; 满足
满足 ,
, ,则数列
,则数列 .
.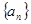 的通项公式
的通项公式 其前
其前 项和
项和 ,则
,则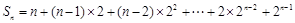 的结果是( )
的结果是( )


