题目内容
18.已知p:关于x的不等式x2+ax-a>0的解集是R,q:-1<a<0,若“p或q”为真“p且q”为假,求a的取值范围.分析 先求出命题p,q为真命题的等价条件,利用“p或q”为真,“p且q”为假,即可求a的取值范围.
解答 解:对于p:若关于x的不等式x2+ax-a>0的解集是R.
则判别式△=a2+4a<0,解得-4<a<0,
即p:-4<a<0,
对于q:-1<a<0,
若“p或q”为真,“p且q”为假,
则p,q一真一假,
若p真q假,则$\left\{\begin{array}{l}{-4<a<0}\\{a≤-1或a≥0}\end{array}\right.$;
解得:-4<a≤-1,
若p假q真,则$\left\{\begin{array}{l}{a≥0或a≤-4}\\{-1<a<0}\end{array}\right.$,无解,
综上:-4<a≤-1.
点评 本题主要考查复合命题与简单命题真假之间的关系,先求出p,q为真时的等价条件是解决本题的关键.

练习册系列答案
相关题目
10.三角形ABC中,边a=$\sqrt{6}$-$\sqrt{2}$,b=4,角C=75°,则△ABC的面积S=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 2$\sqrt{6}$+2 |
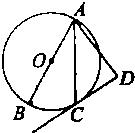 如图,在⊙O中,AB是直径,CD是切线,C为切点,AC平分∠BAD,那么AD和CD的位置关系如何?请证明你的结论.
如图,在⊙O中,AB是直径,CD是切线,C为切点,AC平分∠BAD,那么AD和CD的位置关系如何?请证明你的结论.