题目内容
3．
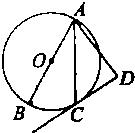如图，在⊙O中，AB是直径，CD是切线，C为切点，AC平分∠BAD，那么AD和CD的位置关系如何？请证明你的结论．
分析 利用圆的切线的性质，角平分线的性质，证明∠DAC=∠OCA，即可得出结论．
解答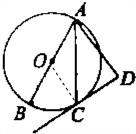 
解：AD⊥CD．
证明如下：连接OC，则OC⊥CD．
∵OA=OC，∴∠OAC=∠OCA，
∵AC平分∠OAD，∴∠DAC=∠OAC，
∴∠DAC=∠OCA，∴OC∥AD．
∵OC⊥CD，∴AD⊥CD
点评 本题考查圆的切线的性质，角平分线的性质，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目