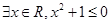题目内容
已知 ,设p:函数
,设p:函数 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,
q:曲线y=x2+(2a 3)x+1与x轴交于不同的两点.若“p且q”为假,“﹁q”为假,求a的取值范围.
 ,设p:函数
,设p:函数 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,q:曲线y=x2+(2a 3)x+1与x轴交于不同的两点.若“p且q”为假,“﹁q”为假,求a的取值范围.
a>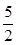 .
.
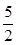 .
.试题分析:求出命题p,q成立的等价条件,然后利用若“p且q”为假,“﹁q”为假,求a的取值范围.
解:p:0<a<1 2分
由Δ=(2a 3)2 4>0,得q:a>
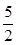 或0
或0 a<
a< . 5分
. 5分 因为“p且q”为假,“﹁q”为假,所以p假q真 7分
即
 ∴a>
∴a>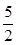 . 10分
. 10分 
练习册系列答案
相关题目
 方程
方程 有两个不等的负实根;
有两个不等的负实根; 方程
方程 无实根.若
无实根.若 或
或 为真,
为真, 的取值范围.
的取值范围.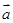 ,
,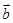 是向量,命题“若
是向量,命题“若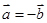 ,则
,则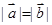 ”的逆命题是( )
”的逆命题是( )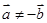 ,则
,则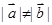
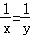 ,则x=y
,则x=y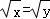
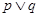 是假命题
是假命题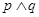 是真命题
是真命题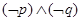 是真命题
是真命题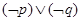 是真命题
是真命题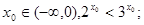 命题
命题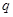 :“
:“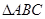 中,若
中,若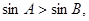 则
则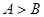 。则下列命题为真命题的是( )
。则下列命题为真命题的是( )



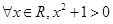 ”的否定是( )
”的否定是( )