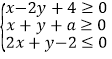题目内容
【题目】已知抛物线![]() 的焦点为F,点
的焦点为F,点![]() 在此抛物线上,
在此抛物线上,![]() ,不过原点的直线
,不过原点的直线![]() 与抛物线C交于A,B两点,以AB为直径的圆M过坐标原点.
与抛物线C交于A,B两点,以AB为直径的圆M过坐标原点.
(1)求抛物线C的方程;
(2)证明:直线![]() 恒过定点;
恒过定点;
(3)若线段AB中点的纵坐标为2,求此时直线![]() 和圆M的方程.
和圆M的方程.
【答案】(1)![]() ;(2)定点
;(2)定点![]() ;(3)
;(3)![]() ,
,![]()
【解析】
(1)根据抛物线的定义,将![]() 转化为抛物线上的点
转化为抛物线上的点![]() 到准线的距离,从而求出
到准线的距离,从而求出![]() ,得到抛物线方程.
,得到抛物线方程.
(2)直线与抛物线联立,得到![]() ,然后利用以
,然后利用以![]() 为直径的圆
为直径的圆![]() 过坐标原点,即
过坐标原点,即![]() ,代入
,代入![]() ,求出斜率与截距的关系,得到直线过的定点.
,求出斜率与截距的关系,得到直线过的定点.
(3)根据![]() 中点坐标,求出直线的斜率,得到直线方程,再求出
中点坐标,求出直线的斜率,得到直线方程,再求出![]() 长度,即圆的半径,得到圆的方程.
长度,即圆的半径,得到圆的方程.
(1)抛物线![]() ,其准线为
,其准线为![]()
![]() 点
点![]() 在此抛物线上,
在此抛物线上,![]() ,
,
![]() 点
点![]() 到准线的距离等于
到准线的距离等于![]() ,即
,即![]() ,得
,得![]()
![]() 所求抛物线方程为
所求抛物线方程为![]()
(2)①当直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为
的方程为![]() ,
,![]() ,易知
,易知![]() .
.
联立方程组得![]() ,从而可得方程
,从而可得方程![]()
由题意可知![]()
![]()
所以![]()
因为以![]() 为直径的圆
为直径的圆![]() 过坐标原点,
过坐标原点,
所以![]() ,即
,即![]() ,所以
,所以![]() ,所以
,所以![]() .
.
所以直线![]() 的方程为
的方程为![]() ,即
,即![]() ,所以直线
,所以直线![]() 恒过定点
恒过定点![]() .
.
②当直线![]() 的斜率不存在时,易求得点
的斜率不存在时,易求得点![]() 坐标分别为
坐标分别为![]() ,
,![]() ,直线
,直线![]() 也过点
也过点![]() .
.
综合①②可知,直线![]() 恒过定点
恒过定点![]() .
.
(3)由题意可知直线![]() 斜率存在,设线段
斜率存在,设线段![]() 中点坐标为
中点坐标为![]()
由(2)中所得![]() ,
,
则![]()
所以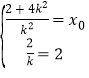 ,解得
,解得![]()
所以直线![]() 方程为
方程为![]() .
.
因为线段![]() 中点坐标为
中点坐标为![]() ,即为圆
,即为圆![]() 的圆心坐标,
的圆心坐标,
设圆![]()
![]() .
.
代入![]() ,得
,得![]()
所以圆![]() 的方程为
的方程为![]()

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】某小学为了解四年级学生的家庭作业用时情况,从本校四年级随机抽取了一批学生进行调查,并绘制了学生作业用时的频率分布直方图,如图所示.
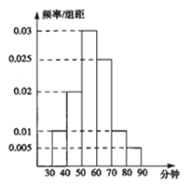
(1)估算这批学生的作业平均用时情况;
(2)作业用时不能完全反映学生学业负担情况,这与学生自身的学习习惯有很大关系如果用时四十分钟之内评价为优异,一个小时以上为一般,其它评价为良好.现从优异和良好的学生里面用分层抽样的方法抽取300人,其中女生有90人(优异20人).请完成列联表,并根据列联表分析能否在犯错误的概率不超过0.05的前提下认为学习习惯与性别有关系?
男生 | 女生 | 合计 | |
良好 | |||
优异 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |