题目内容
【题目】设抛物线![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 作直线
作直线![]() 与抛物线交于
与抛物线交于![]() ,
,![]() 两点,点
两点,点![]() 满足
满足![]() ,过
,过![]() 作
作![]() 轴的垂线与抛物线交于点
轴的垂线与抛物线交于点![]() ,若
,若![]() ,则点
,则点![]() 的横坐标为__________,
的横坐标为__________,![]() __________.
__________.
【答案】1 8
【解析】
利用抛物线的定义,求得![]() 点的坐标,设出直线
点的坐标,设出直线![]() 的方程,联立直线的方程和抛物线的方程,利用韦达定理,求得
的方程,联立直线的方程和抛物线的方程,利用韦达定理,求得![]() 点坐标的表达式,根据
点坐标的表达式,根据![]() 两点的纵坐标相同列方程,解方程求得直线
两点的纵坐标相同列方程,解方程求得直线![]() 的斜率,由此求得
的斜率,由此求得![]() .
.
由于点![]() 满足
满足![]() ,所以
,所以![]() 是线段
是线段![]() 的中点.抛物线的焦点坐标为
的中点.抛物线的焦点坐标为![]() ,准线方程为
,准线方程为![]() .设
.设![]() ,由于
,由于![]() 在抛物线上,且
在抛物线上,且![]() ,根据抛物线的定义得
,根据抛物线的定义得![]() ,所以
,所以![]() ,则
,则![]() ,不妨设
,不妨设![]() .若直线
.若直线![]() 斜率不存在,则
斜率不存在,则![]() ,则
,则![]() ,此时
,此时![]() 的纵坐标和
的纵坐标和![]() 的纵坐标不相同,不符合题意.所以直线
的纵坐标不相同,不符合题意.所以直线![]() 的斜率存在.设
的斜率存在.设![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,代入抛物线方程并化简得
,代入抛物线方程并化简得![]() ,则
,则![]() .由于
.由于![]() 是线段
是线段![]() 中点,所以
中点,所以![]() ,而
,而![]() ,所以
,所以![]() ,即
,即![]() ,即
,即![]() ,解得
,解得![]() .所以
.所以![]() ,所以
,所以![]() ,则
,则![]() 到准线
到准线![]() 的距离为
的距离为![]() ,根据抛物线的定义结合中位线的性质可知
,根据抛物线的定义结合中位线的性质可知![]() .
.
故答案为:(1). 1 (2). 8

 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/oC | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
(Ⅰ)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另3天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]()
(Ⅱ)若由线性回归方程得到的估计数据与所选出的两组检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠.
(参考公式, 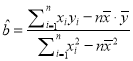 ,
, ![]() ),参考数据
),参考数据![]()
【题目】随着中国教育改革的不断深入,越来越多的教育问题不断涌现.“衡水中学模式”入驻浙江,可以说是应试教育与素质教育的强烈碰撞.这一事件引起了广大市民的密切关注.为了了解广大市民关注教育问题与性别是否有关,记者在北京,上海,深圳随机调查了100位市民,其中男性55位,女性45位.男性中有45位关注教育问题,其余的不关注教育问题;女性中有30位关注教育问题,其余的不关注教育问题.
(1)根据以上数据完成下列2×2列联表;
关注教育问题 | 不关注教育问题 | 合计 | |||||
女 | 30 | 45 | |||||
男 | 45 | 55 | |||||
合计 |
| 100 | |||||
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | ||
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | ||
(2)能否在犯错误的概率不超过0.025的前提下认为是否关注教育与性别有关系?
参考公式: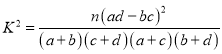 ,其中
,其中![]() .
.