题目内容
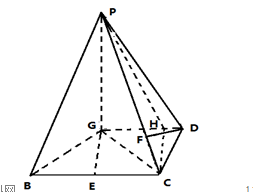
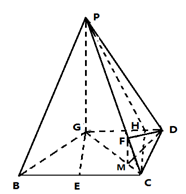
(本小题满分14分)已知四棱锥P—GBCD中(如图),PG⊥平面GBCD,GD∥BC,GD= BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
(Ⅰ)求异面直线GE与PC所成角的余弦值;
(Ⅱ)若F点是棱PC上一点,且 ,
, ,求
,求 的值.
的值.
 BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4
BC,且BG⊥GC,GB=GC=2,E是BC的中点,PG=4(Ⅰ)求异面直线GE与PC所成角的余弦值;
(Ⅱ)若F点是棱PC上一点,且
 ,
, ,求
,求 的值.
的值.
(Ⅰ)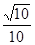 ;(Ⅱ)
;(Ⅱ)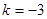
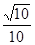 ;(Ⅱ)
;(Ⅱ)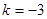
试题分析:(Ⅰ)根据异面直线所成角的定义可过
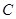 点作
点作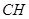 //
//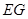 交
交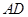 于
于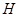 ,则
,则 (或其补角)就是异面直线
(或其补角)就是异面直线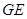 与
与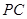 所成的角. 因为
所成的角. 因为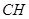 //
//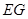 且
且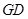 //
//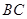 ,则四边形
,则四边形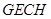 为平行四边形,则
为平行四边形,则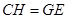 ,
,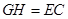 ,故可在
,故可在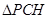 中用余弦定理求
中用余弦定理求 。(Ⅱ)由
。(Ⅱ)由 可得
可得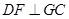 ,过
,过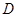 作
作 ,
,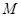 为垂足。易得证
为垂足。易得证 平面
平面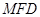 ,可得
,可得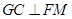 ,从而易得证
,从而易得证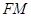 //
// ,可得
,可得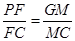 ,即可求
,即可求 的值。
的值。试题解析:(Ⅰ)
在平面
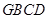 内,过
内,过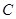 点作
点作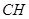 //
//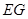 交
交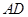 于
于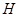 ,连结
,连结 ,则
,则 (或其补角)就是异面直线
(或其补角)就是异面直线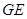 与
与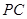 所成的角.
所成的角. 在
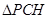 中,
中,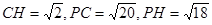
由余弦定理得,
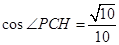
∴异面直线
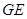 与
与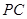 所成角的余弦值为
所成角的余弦值为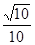 .
.(Ⅱ)
在平面
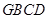 内,过
内,过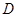 作
作 ,
,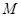 为垂足,连结
为垂足,连结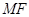 ,又因为
,又因为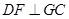
∴
 平面
平面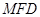 ,
,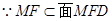 ∴
∴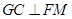
由平面
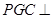 平面
平面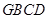 ,∴
,∴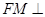 平面
平面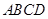 ∴
∴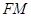 //
//
由
 得
得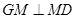 ,∴
,∴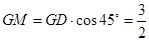
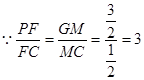 ,∴
,∴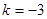 .
.
练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
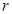 的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?
的一个实心球,使球与水面恰好相切,试求取出球后水面高为多少?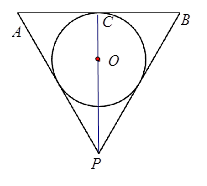

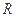 ,球面上
,球面上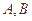 两点都在北纬45°圈上,它们的球面距离为
两点都在北纬45°圈上,它们的球面距离为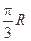 ,
,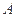 点在东经30°上,则
点在东经30°上,则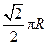
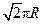
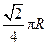
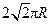
 的铁球,这时水面恰好和球面相切.问将球从圆锥内取出后,圆锥内水平面的高是( )
的铁球,这时水面恰好和球面相切.问将球从圆锥内取出后,圆锥内水平面的高是( )





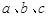 满足
满足 ,
,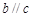 ,则直线
,则直线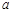 与
与 ( ).
( ).


