Question

【题目】定义实数a，b间的计算法则如下a△b= ．
（1）计算2△（3△1）；
（2）对0＜x＜z＜y的任意实数x，y，z，判断x△（y△z）与（x△y）△z的大小，并说明理由；
（3）写出函数y=（1△x）+（2△x），x∈R的解析式，作出该函数的图象，并写出该函数单调递增区间和值域（只需要写出结果）．

Answer 1

【答案】
（1）解：实数a，b间的计算法则如下a△b= ．

则2△（3△1）=2△3=32=9

（2）解：对0＜x＜z＜y的任意实数x，y，z，

x△（y△z）=x△y=y2，

（x△y）△z=y2△z，

此时若y2≥z，则（x△y）△z=y2；

若y2＜z，则（x△y）△z=z2．

即若y2≥z，则x△（y△z）=（x△y）△z；

若y2＜z，则x△（y△z）＞（x△y）△z

（3）解：当x＞2时，y=（1△x）+（2△x）=x2+x2=2x2；

当1＜x≤2时，y=（1△x）+（2△x）=x2+2；

当x≤1时，y=（1△x）+（2△x）=1+2=3．

即有y= ，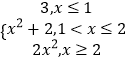

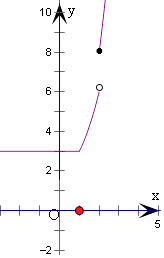
画出函数y的图象，如右：

该函数单调递增区间为（1，2），（2，+∞）；

值域为[3，+∞）．

【解析】（1）先求出3△1，再求出2△（3△1）的值即可；（2）分别求出x△（y△z）和（x△y）△z的值，讨论y2与z的大小即可；（3）讨论x的大小，分x≥2，x＜1，1≤x＜2，求得函数式，画出函数图象，即可得到该函数单调递增区间和值域．