题目内容
【题目】已知函数f(x)=lnx.
(1)求函数g(x)=f(x+1)﹣x的最大值;
(2)若对任意x>0,不等式f(x)≤ax≤x2+1恒成立,求实数a的取值范围;
(3)若x1>x2>0,求证: ![]() >
> ![]() .
.
【答案】
(1)解:∵f(x)=lnx,
∴g(x)=f(x+1)﹣x=ln(x+1)﹣x,x>﹣1,
∴ ![]() .
.
当x∈(﹣1,0)时,g′(x)>0,∴g(x)在(﹣1,0)上单调递增;
当x∈(0,+∞)时,g′(x)<0,则g(x)在(0,+∞)上单调递减,
∴g(x)在x=0处取得最大值g(0)=0
(2)解:∵对任意x>0,不等式f(x)≤ax≤x2+1恒成立,
∴ 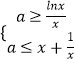 在x>0上恒成立,
在x>0上恒成立,
进一步转化为 ![]() ,
,
设h(x)= ![]() ,则
,则 ![]() ,
,
当x∈(1,e)时,h′(x)>0;当x∈(e,+∞)时,h′(x)<0,
∴h(x) ![]() .
.
要使f(x)≤ax恒成立,必须a ![]() .
.
另一方面,当x>0时,x+ ![]() ,
,
要使ax≤x2+1恒成立,必须a≤2,
∴满足条件的a的取值范围是[ ![]() ,2]
,2]
(3)解:当x1>x2>0时, ![]() >
> ![]() 等价于
等价于 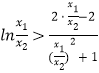 .
.
令t= ![]() ,设u(t)=lnt﹣
,设u(t)=lnt﹣ ![]() ,t>1
,t>1
则 ![]() >0,
>0,
∴u(t)在(1,+∞)上单调递增,
∴u(t)>u(1)=0,
∴ ![]() >
> ![]()
【解析】(1)先求出g(x)=ln(x﹣1)﹣x(x>﹣1),然后求导确定单调区间,极值,最值即可求.(2)本小题转化为 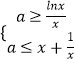 在x>0上恒成立,进一步转化为
在x>0上恒成立,进一步转化为 ![]() ,然后构造函数h(x)=
,然后构造函数h(x)= ![]() ,利用导数研究出h(x)的最大值,再利用基础不等式可知
,利用导数研究出h(x)的最大值,再利用基础不等式可知 ![]() ,从而可知a的取值范围.(3)本小题等价于
,从而可知a的取值范围.(3)本小题等价于 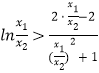 .令t=
.令t= ![]() ,设u(t)=lnt﹣
,设u(t)=lnt﹣ ![]() ,t>1,由导数性质求出u(t)>u(1)=0,由此能够证明
,t>1,由导数性质求出u(t)>u(1)=0,由此能够证明 ![]() >
> ![]() .
.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目