题目内容
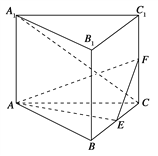
【题目】(2015·湖南)如下图,直三棱柱ABC-A1B1C1的底面是边长为2的正三角形,E、F分别是BC、CC1的中点.
(1)证明:平面AEF⊥平面B1BCC1;
(2)若直线A1C与平面A1ABB1所成的角为45°,求三棱锥F-AEC的体积.
【答案】(1)见解析(2)![]()
【解析】(1)证明:如图,因为三棱柱ABC-A1B1C1是直三棱柱,所以AE⊥BB1,
又E是正三角形ABC的边BC的中点,所以AE⊥BC,因此AE⊥平面B1BCC1,又AE平面AEF,所以平面AEF⊥平面B1BCC1.

(2)设AB的中点为D,连接A1D,CD,因为△ABC是正三角形,所以CD⊥AB,又三棱柱ABC-A1B1C1是直三棱柱,所以CD⊥AA1,因此CD⊥平面A1ABB1,于是∠CA1D为直线A1C与平面A1ABB1所成的角,由题设知∠CA1D=45°,
所以A1D=CD=![]() AB=
AB=![]() ,在Rt△AA1D中,AA1=
,在Rt△AA1D中,AA1=![]()
![]() ,所以FC=
,所以FC=![]() AA1=
AA1=![]() ,故三棱锥F-AEC的体积V=
,故三棱锥F-AEC的体积V=
![]() S△AEC×FC=
S△AEC×FC=![]() .
.

练习册系列答案
相关题目
【题目】为了了解某城市居民用水量的情况,我们获得100位居民某年的月均用水量(单位:吨)通过对数据的处理,我们获得了该100位居民月均用水量的频率分布表,并绘制了频率分布直方图(部分数据隐藏)
100位居民月均用水量的频率分布表
组号 | 分组 | 频数 | 频率 |
1 |
| 4 | 0.04 |
2 |
| 0.08 | |
3 |
| 15 | |
4 |
| 22 | |
5 |
|
| |
6 |
| 14 | 0.14 |
7 |
| 6 |
|
8 |
| 4 | 0.04 |
9 |
| 0.02 | |
合 计 | 100 | ||

(1)确定表中![]() 与
与![]() 的值;
的值;
(2)求频率分布直方图中左数第4个矩形的高度;
(3)在频率分布直方图中画出频率分布折线图;
(4)我们想得到总体密度曲线,请回答我们应该怎么做?
