题目内容
【题目】已知![]() 的顶点
的顶点![]() ,
, ![]() 边上的中线
边上的中线![]() 所在直线方程为
所在直线方程为![]() ,
, ![]() 边上的高
边上的高![]() 所在直线方程为
所在直线方程为![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)求直线![]() 的方程.
的方程.
【答案】(1) C(5,3);(2) 6x-5y-15=0.
【解析】试题分析:(1)已知![]() 边上的高
边上的高![]() 所在直线方程,可得
所在直线方程,可得![]() 所在直线的斜率,联立
所在直线的斜率,联立![]() 和
和![]() 的直线方程即可求出点
的直线方程即可求出点![]() 的坐标(2)
的坐标(2)![]() 所在直线方程是
所在直线方程是![]() 边上的中线所在直线方程,则
边上的中线所在直线方程,则![]() 的中点坐标满足此直线方程,代入直线方程求得B 点所在直线方程联立直线方程求出B(0,-3),即可求出直线
的中点坐标满足此直线方程,代入直线方程求得B 点所在直线方程联立直线方程求出B(0,-3),即可求出直线![]() 的方程
的方程
解析:(1)依题意知:kAC=-2,A(6,1),
∴lAC为2x+y-13=0,
联立lAC、lCM得![]() ∴C(5,3).
∴C(5,3).
(2)设B(x0,y0),AB的中点M为(![]() ,
,![]() ),
),
代入2x-y-7=0,得2x0-y0-3=0,
∴![]() ∴B(0,-3),
∴B(0,-3),
∴kBC=![]() ,∴直线BC的方程为y=
,∴直线BC的方程为y=![]() x-3,
x-3,
即6x-5y-15=0.

【题目】从某企业生产的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
频数 | 6 | 26 | 38 | 22 | 8 |
(1)作出这些数据的频率分布直方图;
(2)估计这种产品质量指标值的平均数及方差(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定?
【题目】某市积极倡导学生参与绿色环保活动,其中代号为“环保卫士—12369”的绿色环保活动小组对2014年1月—2014年12月(一年)内空气质量指数![]() 进行监测,下表是在这一年随机抽取的100天的统计结果:
进行监测,下表是在这一年随机抽取的100天的统计结果:
指数API | [0,50] | (50,100] | (100,150] | (150,200] | (200,250] | (250,300] | >300 |
空气质量 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 中重度污染 | 重度污染 |
天数 | 4 | 13 | 18 | 30 | 9 | 11 | 15 |
(1)若某市某企业每天由空气污染造成的经济损失![]() (单位:元)与空气质量指数
(单位:元)与空气质量指数![]() (记为
(记为![]() )的关系为:
)的关系为: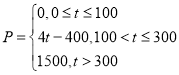 ,在这一年内随机抽取一天,估计该天经济损失
,在这一年内随机抽取一天,估计该天经济损失![]() 元的概率;
元的概率;
(2)若本次抽取的样本数据有30天是在供暖季节,其中有8天为重度污染,![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为某市本年度空气重度污染与供暖有关?
的把握认为某市本年度空气重度污染与供暖有关?
非重度污染 | 重度污染 | 合计 | |
供暖季 | |||
非供暖季节 | |||
合计 | 100 |
下面临界值表供参考.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.