题目内容
【题目】已知f(x)=xlnx,g(x)=x3+ax2﹣x+2
(1)求函数f(x)的单调区间;
(2)求函数f(x)在[t,t+2](t>0)上的最小值;
(3)对一切的x,2f(x)≤g′(x)+2恒成立,求实数a的取值范围.
【答案】
(1)解:f′(x)=lnx+1令f′(x)<0解得0<x< ![]() ,
,
∴f(x)的单调递减区间为(0, ![]() )
)
令f′(x)>0解得x> ![]() ,
,
∴f(x)的单调递增区间为( ![]() ,+∞)
,+∞)
(2)解:当0<t<t+2< ![]() 时,t无解
时,t无解
当0<t≤ ![]() <t+2,即0<t≤
<t+2,即0<t≤ ![]() 时,
时,
∴f(x)min=f( ![]() )=﹣
)=﹣ ![]() ;
;
当 ![]() <t<t+2,即t>
<t<t+2,即t> ![]() 时,f(x)在[t,t+2]上单调递增,
时,f(x)在[t,t+2]上单调递增,
∴f(x)min=f(t)=tlnt
∴f(x)min= 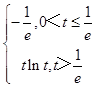
(3)解:由题意:2xlnx≤3x2+2ax﹣1+2即2xlnx≤3x2+2ax+1
∵x∈(0,+∞)
∴a≥lnx﹣ ![]() x﹣
x﹣ ![]() ,
,
设h(x)=lnx﹣ ![]() x﹣
x﹣ ![]() ,
,
则h′(x)= ![]() ﹣
﹣ ![]() +
+ ![]() =﹣
=﹣ ![]() ,
,
令h′(x)=0,得x=1,x=﹣ ![]() (舍)
(舍)
当0<x<1时,h′(x)>0;当x>1时,h′(x)<0
∴当x=1时,h(x)取得最大值,h(x)max=﹣2
∴a≥﹣2
故实数a的取值范围[﹣2,+∞)
【解析】(1)求出f′(x),令f′(x)小于0求出x的范围即为函数的减区间,令f′(x)大于0求出x的范围即为函数的增区间;(2)当0<t<t+2< ![]() 时t无解,当0<t≤
时t无解,当0<t≤ ![]() <t+2即0<t≤
<t+2即0<t≤ ![]() 时,根据函数的增减性得到f(x)的最小值为f(
时,根据函数的增减性得到f(x)的最小值为f( ![]() ),当
),当 ![]() <t<t+2即t>
<t<t+2即t> ![]() 时,函数为增函数,得到f(x)的最小值为f(t);(3)求出g′(x),把f(x)和g′(x)代入2f(x)≤g′(x)+2中,根据x大于0解出a≥lnx﹣
时,函数为增函数,得到f(x)的最小值为f(t);(3)求出g′(x),把f(x)和g′(x)代入2f(x)≤g′(x)+2中,根据x大于0解出a≥lnx﹣ ![]() x﹣
x﹣ ![]() ,然后令h(x)=lnx﹣
,然后令h(x)=lnx﹣ ![]() x﹣
x﹣ ![]() ,求出h(x)的最大值,a大于等于h(x)的最大值,方法是先求出h′(x)=0时x的值,利用函数的定义域和x的值分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性即可得到函数的最大值,即可求出a的取值范围.
,求出h(x)的最大值,a大于等于h(x)的最大值,方法是先求出h′(x)=0时x的值,利用函数的定义域和x的值分区间讨论导函数的正负得到函数的单调区间,根据函数的增减性即可得到函数的最大值,即可求出a的取值范围.
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.

【题目】厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x/元 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y/件 | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求线性回归方程![]() =
=![]() x+
x+![]() ,其中
,其中![]() =-20,
=-20, ![]() =
=![]() -
-![]()
![]() .
.
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)