题目内容

【题目】已知直线及点.

（1）证明直线过某定点，并求该定点的坐标；

（2）当点到直线的距离最大时，求直线的方程.

【答案】(1)证明见解析，定点坐标为；(2)15x＋24y＋2＝0.

【解析】试题分析：（1）直线l的方程可化为 a(2x＋y＋1)＋b(－x＋y－1)＝0，由，即可解得定点；

（2）由（1）知直线l恒过定点A，当直线l垂直于直线PA时，点P到直线l的距离最大，利用点斜式求直线方程即可.

试题解析：

（1）证明：直线l的方程可化为 a(2x＋y＋1)＋b(－x＋y－1)＝0，

由，

得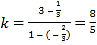，所以直线l恒过定点．

（2）由（1）知直线l恒过定点A，

当直线l垂直于直线PA时，点P到直线l的距离最大．

又直线PA的斜率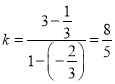，所以直线l的斜率kl＝－．

故直线l的方程为，

即15x＋24y＋2＝0．

练习册系列答案
相关题目

【题目】设集合A={x|x2+2x﹣3＜0}，集合B={x||x+a|＜1}．
（1）若a=3，求A∪B；
（2）设命题p：x∈A，命题q：x∈B，若p是q成立的必要不充分条件，求实数a的取值范围．

【题目】已知f（x）=xlnx，g（x）=x3+ax2﹣x+2
（1）求函数f（x）的单调区间；
（2）求函数f（x）在[t，t+2]（t＞0）上的最小值；
（3）对一切的x，2f（x）≤g′（x）+2恒成立，求实数a的取值范围．

【题目】判断下列结论的正误（正确的打“√”，错误的打“×”）．

（）在增函数与减函数的定义中，可以把“任意两个自变量”改为“存在两个自变量”．_____

（）函数的单调递减区间是．_____

（）所有的单调函数都有最值．_______

（）与表示同一个集合．______

（）已知定义在上的函数的图象是连续不断的，当时，则方程至少有一个实数解．_______

【题目】在△ABC中，内角A，B，C所对的边分别为a，b，c，已知cosB= ，tanC= ． （Ⅰ）求tanB和tanA；
（Ⅱ）若c=1，求△ABC的面积．

【题目】设数列{an}的前n项和为Sn ， 且Sn=2﹣an ， n∈N* ， 设函数f（x）=log x，数列{bn}满足bn=f（an），记{bn}的前n项和为Tn ． （Ⅰ）求an及Tn；
（Ⅱ）记cn=anbn ， 求cn的最大值．

【题目】函数f（x）=x2+bx﹣1（b∈R）．
（1）若函数y=f（x）在[1，+∞）上单调，求b的取值范围；
（2）若函数y=|f（x）|﹣2有四个零点，求b的取值范围；
（3）若函数y=|f（x）|在[0，|b|）上的最大值为g（b），求g（b）的表达式．

【题目】已知f（x）=x3+3ax2+bx+a2（a＞1）在x=﹣1时有极值0．
（1）求常数 a，b的值；
（2）方程f（x）=c在区间[﹣4，0]上有三个不同的实根时，求实数c的范围．

【题目】已知平行四边形ABCD的三个顶点的坐标为A（﹣1，5），B（﹣2，﹣1），C（2，3）．

（1）求平行四边形ABCD的顶点D的坐标；
（2）在△ACD中，求CD边上的高所在直线方程；
（3）求四边形ABCD的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网