Question

【题目】已知函数f（x）＝（2－a）（x－1）－2lnx（a∈R）．

（1）若曲线g（x）＝f（x）＋x上点（1，g（1））处的切线过点（0，2），求函数g（x）的单调减区间；

（2）若函数y＝f（x）在区间（0， ）内无零点，求实数a的最小值．

Answer 1

【答案】（1）函数在(0,2)上递减（2）函数在上无零点，a的最小值为2-4ln2

【解析】试题分析：（1）求出函数的导数，计算g′（1），求出a的值，从而求出g（x）的递减区间即可；

（2）问题转化为对x∈（0， ），a＞2﹣恒成立，令l（x）=2﹣，x∈（0， ），根据函数的单调性求出a的最小值即可．

试题解析：

（1）∵g（x）=（3﹣a）x﹣（2﹣a）﹣2lnx，

∴g′（x）=3﹣a﹣，∴g′（1）=1﹣a，

又g（1）=1，∴1﹣a==﹣1，解得：a=2，

由g′（x）=3﹣2﹣=＜0，解得：0＜x＜2，

∴函数g（x）在（0，2）递减；

（2）∵f（x）＜0在（0， ）恒成立不可能，

故要使f（x）在（0， ）无零点，只需任意x∈（0， ），f（x）＞0恒成立，

即对x∈（0， ），a＞2﹣恒成立，

令h（x）=2﹣，x∈（0， ），

则h′（x）=，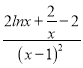

再令m（x）=﹣2，x∈（0， ），

则m′（x）=＜0，

故m（x）在（0， ）递减，于是m（x）＞m（）=2﹣2ln2＞0，

从而h′（x）＞0，于是h（x）在（0， ）递增，

∴h（x）＜h（）=2﹣4ln2，

故要使a＞2﹣恒成立，只要a∈[2﹣4ln2，+∞），

综上，若函数y=f（x）在（0， ）上无零点，则a的最小值是2﹣4ln2．