题目内容
函数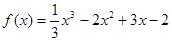 在区间
在区间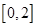 上最大值与最小值的和为
上最大值与最小值的和为
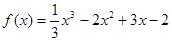 在区间
在区间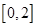 上最大值与最小值的和为
上最大值与最小值的和为 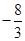
试题分析:根据题意,由于
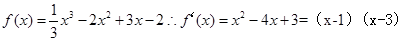 ,故可知当0<x<1,递增,在1<x<2时函数递减,故可知函数在区间
,故可知当0<x<1,递增,在1<x<2时函数递减,故可知函数在区间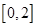 上最大值与最小值分别是
上最大值与最小值分别是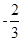 ,-2,故可知和为
,-2,故可知和为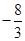 ,故答案为
,故答案为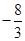 。
。点评:主要是考查了导数在研究函数最值中的运用,属于基础题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
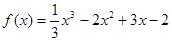 在区间
在区间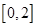 上最大值与最小值的和为
上最大值与最小值的和为 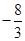
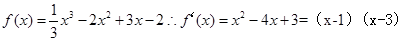 ,故可知当0<x<1,递增,在1<x<2时函数递减,故可知函数在区间
,故可知当0<x<1,递增,在1<x<2时函数递减,故可知函数在区间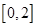 上最大值与最小值分别是
上最大值与最小值分别是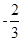 ,-2,故可知和为
,-2,故可知和为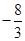 ,故答案为
,故答案为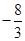 。
。
 阅读快车系列答案
阅读快车系列答案