题目内容
如图,在等边△ABC中,P是边AC上一点,连接BP,将△BCP绕点B逆时针旋转60°,得到△BAQ,连接PQ.若BC=8,BP=7,则△APQ的周长是 .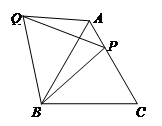
15
试题分析:根据题意可知,在△APQ中,
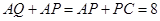 ,又因为BP=7,
,又因为BP=7,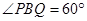 ,所以
,所以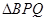 为正三角形,所以
为正三角形,所以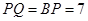 ,所以该三角形的周长为15.
,所以该三角形的周长为15.点评:对于此类问题,要充分发挥空间想象能力,抓住折叠、旋转过程中的变量和不变量.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
题目内容
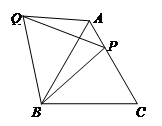
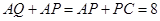 ,又因为BP=7,
,又因为BP=7,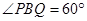 ,所以
,所以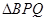 为正三角形,所以
为正三角形,所以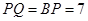 ,所以该三角形的周长为15.
,所以该三角形的周长为15.
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案