题目内容
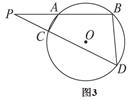
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.

(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
(1)证明同位角相等。CD∥AB.
(2)证得∠AFG+∠GBA=180°.说明A,B,G,F四点共圆.
(2)证得∠AFG+∠GBA=180°.说明A,B,G,F四点共圆.
试题分析: (1)因为EC=ED,所以∠EDC=∠ECD.
因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA.
故∠ECD=∠EBA.
所以CD∥AB.

(2)由(1)知,AE=BE.因为EF=EG,故∠EFD=∠EGC,从而∠FED=∠GEC.
连结AF,BG,则△EFA≌△EGB,故∠FAE=∠GBE.
又CD∥AB,∠EDC=∠ECD,所以∠FAB=∠GBA.
所以∠AFG+∠GBA=180°.
故A,B,G,F四点共圆.
点评:中档题,涉及圆的问题,往往与三角形相关联,利用三角形相似或三角形全等解决问题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
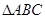 的外接圆,
的外接圆, 是
是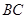 边上的高,
边上的高,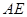 是⊙O的直径.
是⊙O的直径.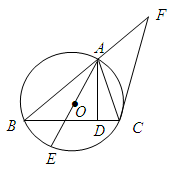
 ;
;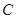 作⊙O的切线交
作⊙O的切线交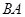 的延长线于点
的延长线于点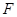 ,若
,若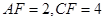 ,求
,求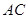 的长.
的长.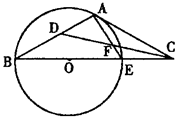
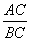 的值.
的值.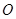 的直径
的直径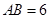 ,
,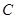 为圆周上一点,
为圆周上一点,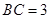 ,过
,过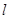 ,
,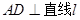 于点
于点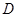 ,交⊙
,交⊙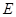 ,则
,则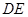 的长为 .
的长为 .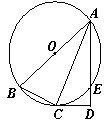
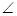 AMB=30o,那么⊙O2的半径为 ;
AMB=30o,那么⊙O2的半径为 ;
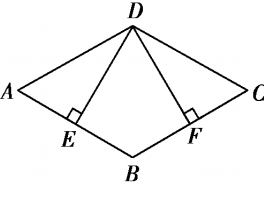
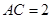 ,则BD等于
,则BD等于