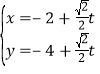题目内容
【题目】已知数列![]() 中
中![]() ,前
,前![]() 项和为
项和为![]() ,若对任意的
,若对任意的![]() ,均有
,均有![]() (
(![]() 是常数,且
是常数,且![]() )成立,则称数列
)成立,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)若数列![]() 为“
为“![]() 数列”,求数列
数列”,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(2)若数列![]() 为“
为“![]() 数列”,且
数列”,且![]() 为整数,试问:是否存在数列
为整数,试问:是否存在数列![]() ,使得
,使得![]() 对一切
对一切![]() ,
,![]() 恒成立?如果存在,求出这样数列
恒成立?如果存在,求出这样数列![]() 的
的![]() 的所有可能值,如果不存在,请说明理由;
的所有可能值,如果不存在,请说明理由;
(3)若数列![]() 为“
为“![]() 数列”,且
数列”,且![]() ,证明:
,证明:![]() .
.
【答案】(1)![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)由和项与通项关系得![]() ,再根据等比数列定义以及等比数列求和公式求结果,(2)由和项与通项关系得
,再根据等比数列定义以及等比数列求和公式求结果,(2)由和项与通项关系得![]() ,代入化简得
,代入化简得![]() ,即得
,即得![]() ,再化为
,再化为![]() ,解得
,解得![]() 的所有可能值,(3)由和项与通项关系得
的所有可能值,(3)由和项与通项关系得![]() ,根据条件可得数列不减,得
,根据条件可得数列不减,得![]() ,叠放得
,叠放得![]() ,从而
,从而![]() ,而
,而![]() ,所以得证.
,所以得证.
试题解析:(1)数列![]() 为“
为“![]() 数列”,则
数列”,则![]() ,故
,故![]() ,
,
两式相减得:![]() ,
,
又![]() 时,
时,![]() ,所以
,所以![]()
故![]() 对任意的
对任意的![]() 恒成立,即
恒成立,即![]() (常数),
(常数),
故数列![]() 为等比数列,其通项公式为
为等比数列,其通项公式为![]() ;
;
![]() .
.
(2)![]()
![]()
当![]() 时,
时,![]()
因为![]() ,则
,则![]() ;
;
则![]()
则![]() ,因为
,因为![]()
则![]()
因为![]() ,则
,则![]() ,且
,且![]() 时,
时,![]() ,
,
解得:![]() .
.
(3)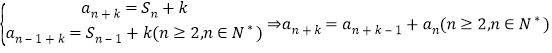
![]() ,由归纳知,
,由归纳知,![]() ,
,
![]() ,由归纳知,
,由归纳知,![]() ,
,
则![]()
![]()
![]()
于是![]()
于是![]()
![]() ,∴
,∴![]()
结论显然成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】[2018·临川一中]海盗船是一种绕水平轴往复摆动的游乐项目,因其外形仿照古代海盗船而得名.现有甲、乙两游乐场统计了一天6个时间点参与海盗船游玩的游客数量,具体数据如表:
时间点 | 8点 | 10点 | 12点 | 14点 | 16点 | 18点 |
甲游乐场 | 10 | 3 | 12 | 6 | 12 | 20 |
乙游乐场 | 13 | 4 | 3 | 2 | 6 | 19 |
(1)从所给6个时间点中任选一个,求参与海盗船游玩的游客数量甲游乐场比乙游乐场少的概率;
(2)记甲、乙两游乐场6个时间点参与海盗船游玩的游客数量分别为![]() ,
,![]() (
(![]() ),现从该6个时间点中任取2个,求恰有1个时间点满足
),现从该6个时间点中任取2个,求恰有1个时间点满足![]() 的概率.
的概率.