题目内容
(本小题满分13分)
已知数列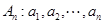
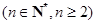 满足
满足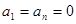 ,且当
,且当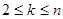
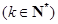 时,
时,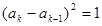 ,令
,令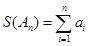 .
.
(Ⅰ)写出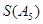 的所有可能的值;
的所有可能的值;
(Ⅱ)求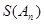 的最大值;
的最大值;
(Ⅲ)是否存在数列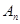 ,使得
,使得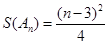 ?若存在,求出数列
?若存在,求出数列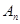 ;若不存在,说明理由.
;若不存在,说明理由.
已知数列
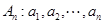
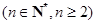 满足
满足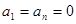 ,且当
,且当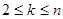
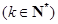 时,
时,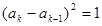 ,令
,令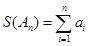 .
.(Ⅰ)写出
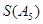 的所有可能的值;
的所有可能的值;(Ⅱ)求
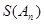 的最大值;
的最大值;(Ⅲ)是否存在数列
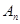 ,使得
,使得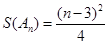 ?若存在,求出数列
?若存在,求出数列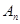 ;若不存在,说明理由.
;若不存在,说明理由.(1)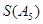 的所有可能的值为:
的所有可能的值为: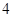 ,
,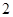 ,
, ,
,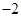 ,
,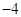 .(2)
.(2)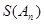 的最大值为
的最大值为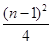 ;(3)
;(3)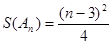 .
.
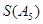 的所有可能的值为:
的所有可能的值为: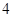 ,
,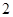 ,
, ,
,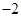 ,
,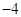 .(2)
.(2)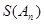 的最大值为
的最大值为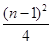 ;(3)
;(3)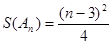 .
.第一问中,根据题意可知当i=5时,满足条件的数列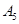 的所有可能情况有
的所有可能情况有
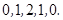
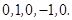
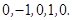 ,分别结算得到
,分别结算得到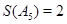
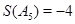
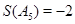 的值
的值
第二问中,因为递推关系可知由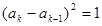 ,
,
可设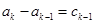 ,则
,则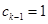 或
或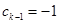 (
(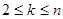 ,
,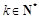 ),
),
那么借助于累加法的思想得到数列的通项公式
第三问中,由(Ⅱ)可知,如果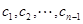 的前
的前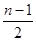 项中恰有
项中恰有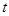 项
项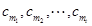 取
取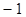 ,
,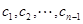 的后
的后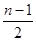 项中恰有
项中恰有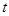 项
项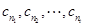 取
取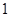 ,则
,则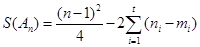 ,可知分析得到结论。
,可知分析得到结论。
解:(Ⅰ)由题设,满足条件的数列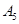 的所有可能情况有:
的所有可能情况有:
(1)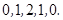 此时
此时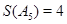 ;(2)
;(2)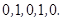 此时
此时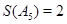 ;
;
(3)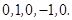 此时
此时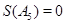 ;(4)
;(4)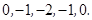 此时
此时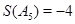 ;
;
(5)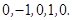 此时
此时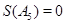 ;(6)
;(6)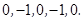 此时
此时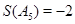 ;
;
所以,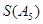 的所有可能的值为:
的所有可能的值为: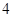 ,
,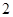 ,
, ,
,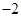 ,
,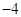 . ……4分
. ……4分
(Ⅱ)由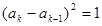 ,
,
可设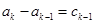 ,则
,则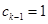 或
或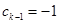 (
(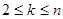 ,
,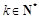 ),
),
因为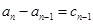 ,所以
,所以 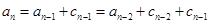
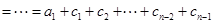 .
.
因为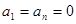 ,所以
,所以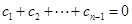 ,且
,且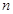 为奇数,
为奇数,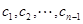 是由
是由
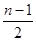 个1和
个1和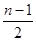 个
个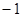 构成的数列
构成的数列
所以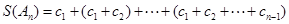
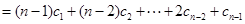 .
.
则当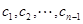 的前
的前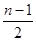 项取
项取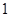 ,后
,后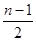 项取
项取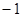 时
时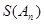 最大,
最大,
此时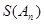
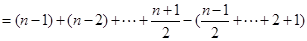
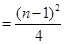 .
.
证明如下:
假设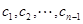 的前
的前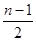 项中恰有
项中恰有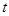 项
项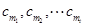 取
取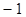 ,则
,则
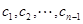 的后
的后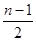 项中恰有
项中恰有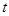 项
项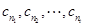 取
取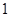 ,其中
,其中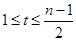 ,
,
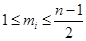 ,
,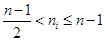 ,
,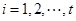 .
.
所以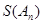
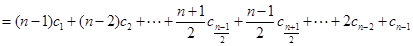
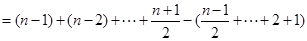
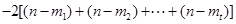
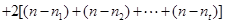
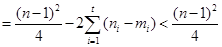 .
.
所以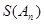 的最大值为
的最大值为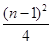 . ……9分
. ……9分
(Ⅲ)由(Ⅱ)可知,如果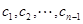 的前
的前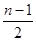 项中恰有
项中恰有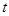 项
项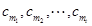 取
取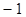 ,
,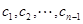 的后
的后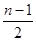 项中恰有
项中恰有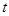 项
项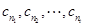 取
取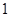 ,则
,则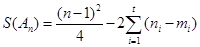 ,若
,若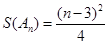 ,则
,则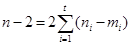 ,因为
,因为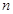 是奇数,所以
是奇数,所以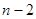 是奇数,而
是奇数,而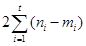 是偶数,因此不存在数列
是偶数,因此不存在数列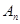 ,使得
,使得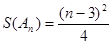 . ……13分
. ……13分
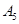 的所有可能情况有
的所有可能情况有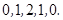
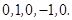
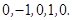 ,分别结算得到
,分别结算得到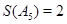
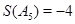
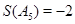 的值
的值第二问中,因为递推关系可知由
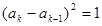 ,
,可设
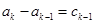 ,则
,则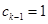 或
或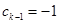 (
(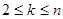 ,
,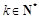 ),
),那么借助于累加法的思想得到数列的通项公式
第三问中,由(Ⅱ)可知,如果
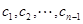 的前
的前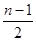 项中恰有
项中恰有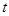 项
项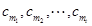 取
取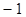 ,
,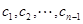 的后
的后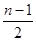 项中恰有
项中恰有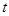 项
项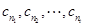 取
取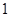 ,则
,则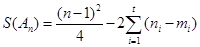 ,可知分析得到结论。
,可知分析得到结论。解:(Ⅰ)由题设,满足条件的数列
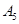 的所有可能情况有:
的所有可能情况有:(1)
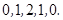 此时
此时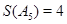 ;(2)
;(2)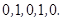 此时
此时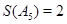 ;
;(3)
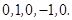 此时
此时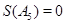 ;(4)
;(4)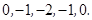 此时
此时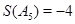 ;
;(5)
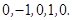 此时
此时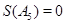 ;(6)
;(6)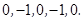 此时
此时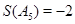 ;
;所以,
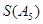 的所有可能的值为:
的所有可能的值为: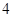 ,
,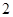 ,
, ,
,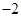 ,
,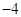 . ……4分
. ……4分(Ⅱ)由
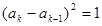 ,
,可设
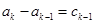 ,则
,则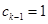 或
或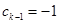 (
(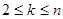 ,
,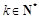 ),
),因为
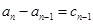 ,所以
,所以 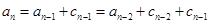
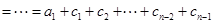 .
.因为
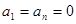 ,所以
,所以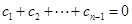 ,且
,且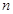 为奇数,
为奇数,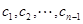 是由
是由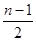 个1和
个1和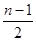 个
个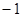 构成的数列
构成的数列所以
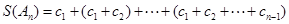
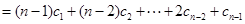 .
.则当
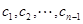 的前
的前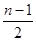 项取
项取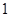 ,后
,后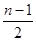 项取
项取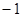 时
时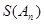 最大,
最大,此时
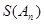
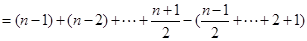
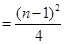 .
.证明如下:
假设
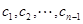 的前
的前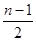 项中恰有
项中恰有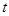 项
项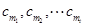 取
取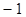 ,则
,则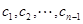 的后
的后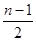 项中恰有
项中恰有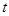 项
项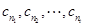 取
取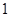 ,其中
,其中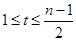 ,
,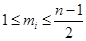 ,
,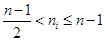 ,
,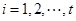 .
.所以
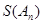
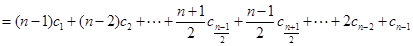
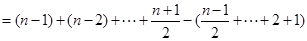
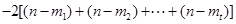
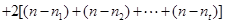
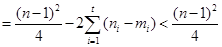 .
.所以
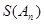 的最大值为
的最大值为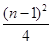 . ……9分
. ……9分(Ⅲ)由(Ⅱ)可知,如果
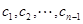 的前
的前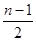 项中恰有
项中恰有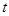 项
项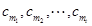 取
取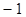 ,
,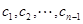 的后
的后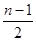 项中恰有
项中恰有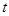 项
项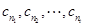 取
取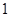 ,则
,则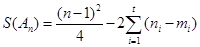 ,若
,若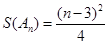 ,则
,则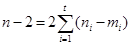 ,因为
,因为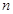 是奇数,所以
是奇数,所以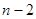 是奇数,而
是奇数,而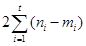 是偶数,因此不存在数列
是偶数,因此不存在数列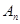 ,使得
,使得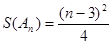 . ……13分
. ……13分
练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
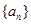 的前
的前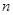 项和为
项和为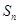 ,
,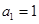 ,
,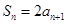 ,,则
,,则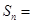
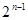
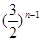
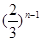
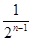
 是首项为
是首项为 的等比数列,且满足
的等比数列,且满足
 .
. 的值和数列
的值和数列 项、……,余下的项按原来的顺序组成一个新的数列
项、……,余下的项按原来的顺序组成一个新的数列 ,试写出数列
,试写出数列 项和为
项和为 .是否存在正整数
.是否存在正整数 ?若存在,试求所有满足条件的正整数
?若存在,试求所有满足条件的正整数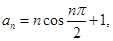 ,前n项和为Sn,则S2012=___________
,前n项和为Sn,则S2012=___________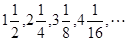 前n项的和为 ( )
前n项的和为 ( )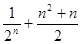
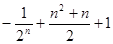
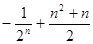
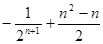
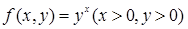 ,已知数列
,已知数列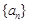 满足:
满足: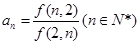 ,若对任意正整数
,若对任意正整数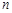 ,都有
,都有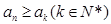 成立,则
成立,则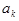 的值为 .
的值为 . 的前
的前 项和
项和 ,求
,求
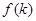 ,使其满足:①
,使其满足:①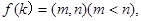 且
且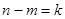 ;
;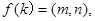 那么
那么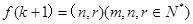 .若已知
.若已知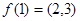 ,则
,则 ;
; .
. 满足
满足 且
且 ,则此数列第5项是
,则此数列第5项是