题目内容
【题目】在![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 是
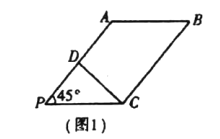
是![]() 中点(如图1).将
中点(如图1).将![]() 沿
沿![]() 折起到图2中
折起到图2中![]() 的位置,得到四棱锥
的位置,得到四棱锥![]() .
.
(1)将![]() 沿
沿![]() 折起的过程中,
折起的过程中, ![]() 平面
平面![]() 是否成立?并证明你的结论;
是否成立?并证明你的结论;
(2)若![]() 与平面
与平面![]() 所成的角为60°,且
所成的角为60°,且![]() 为锐角三角形,求平面
为锐角三角形,求平面![]() 和平面
和平面![]() 所成角的余弦值.
所成角的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)当DP1⊥DA时,CD⊥平面P1DA.由余弦定理得DC2=4,由勾股定理得DC⊥AD.即得到将△PCD沿CD折起的过程中,当DP1⊥DA时,CD⊥平面P1DA.(2)先证明![]() 在平面
在平面![]() 内的射影
内的射影![]() 必在棱
必在棱![]() 上,再建系,得到两个平面的法向量,得到两个法向量的夹角进而得到两个面的夹角。
上,再建系,得到两个平面的法向量,得到两个法向量的夹角进而得到两个面的夹角。
解析:
(1)将![]() 沿
沿![]() 折起过程中,
折起过程中, ![]() 平面
平面![]() 成立,
成立,
证明:∵![]() 是
是![]() 中点,∴
中点,∴![]() ,
,
在![]() 中,由余弦定理得,
中,由余弦定理得,
![]()
![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形且
为等腰直角三角形且![]() ,
,
∴![]() ,
, ![]() ,
, ![]()
∴![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ,
,
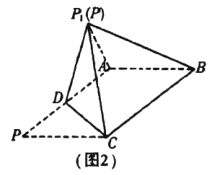
∵![]() 为锐角三角形,∴
为锐角三角形,∴![]() 在平面
在平面![]() 内的射影
内的射影![]() 必在棱
必在棱![]() 上(如图),
上(如图),
∴![]() 平面
平面![]() ,
,
则![]() 是
是![]() 和平面
和平面![]() 所成的角,
所成的角,
故![]() ,
,
∵![]() ,
,
∴![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 中点,
中点,
故以![]() 为坐标原点,过点
为坐标原点,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴建立如图所示坐标系.
轴建立如图所示坐标系.

设![]() 轴于
轴于![]() 交于点
交于点![]() ,
,
∵![]() ,∴
,∴ ![]() ,
,
易知![]() ,
,
∴![]() ,
,
则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∵![]() 平面
平面![]() ,
,
∴可取平面![]() 的法向量
的法向量![]() ,
,
设平面![]() 的法向量
的法向量![]() ,平面
,平面![]() 和平面
和平面![]() 所成的角为
所成的角为![]() ,
,
则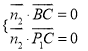 ,∴
,∴ 得
得
令![]() ,则
,则 ,
,
从而 .
.

 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
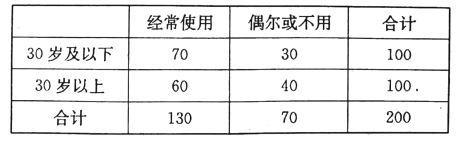
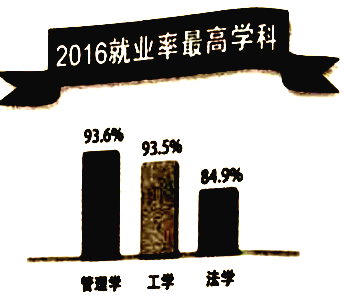
金状元绩优好卷系列答案【题目】某网站调查2016年大学毕业生就业状况,其中一项数据显示“2016年就业率最高学科”为管理学,高达![]() (数据来源于网络,仅供参考).为了解高三学生对“管理学”的兴趣程度,某校学生社团在高校高三文科班进行了问卷调查,问卷共100道选择题,每题1分,总分100分,社团随机抽取了100名学生的问卷成绩(单位:分)进行统计,得到频率分布表如下:
(数据来源于网络,仅供参考).为了解高三学生对“管理学”的兴趣程度,某校学生社团在高校高三文科班进行了问卷调查,问卷共100道选择题,每题1分,总分100分,社团随机抽取了100名学生的问卷成绩(单位:分)进行统计,得到频率分布表如下:
组号 | 分组 | 男生 | 女生 | 频数 | 频率 |
第一组 |
| 3 | 2 | 5 | 0.05 |
第二组 |
| 17 |
|
|
|
第三组 |
| 20 | 10 | 30 | 0.3 |
第四组 |
| 6 | 18 | 24 | 0.24 |
第五组 |
| 4 | 12 | 16 | 0.16 |
合计 | 50 | 50 | 100 | 1 | |
(1)求频率分布表中![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)若将得分不低于60分的称为“管理学意向”学生,将低于60分的称为“非管理学意向”学生,根据条件完成下面![]() 列联表,并据此判断是否有
列联表,并据此判断是否有![]() 的把握认为是否为“管理学意向”与性别有关?
的把握认为是否为“管理学意向”与性别有关?
非管理学意向 | 管理学意向 | 合计 | |
男生 |
|
| |
女生 |
|
| |
合计 |
(3)心理咨询师认为得分低于20分的学生可能“选择困难”,要从“选择困难”的5名学生中随机抽取2名学生进行心理辅导,求恰好有1名男生,1名女生被选中的概率.
参考公式: 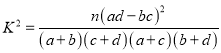 ,其中
,其中![]() .
.
参考临界值:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |