题目内容
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线
轴的正半轴为极轴,取相同的长度单位建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,求曲线
时,求曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值;
的距离的最大值;
(2)若曲线![]() 上的所有点都在直线
上的所有点都在直线![]() 的下方,求实数
的下方,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:
(1)由题意结合点到直线距离公式可得距离的解析式为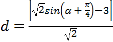 ,结合三角函数的性质可得曲线
,结合三角函数的性质可得曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
(2)原问题等价于对![]() ,有
,有![]() 恒成立,结合恒成立的条件可得实数
恒成立,结合恒成立的条件可得实数![]() 的取值范围是
的取值范围是![]() .
.
试题解析:
(1)直线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
曲线![]() 上的点到直线
上的点到直线![]() 的距离
的距离
![]()
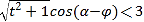 ,
,
当![]() 时,
时, 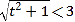 ,
,
即曲线![]() 上的点到直线
上的点到直线![]() 的距离的最大值为
的距离的最大值为![]() .
.
(2)∵曲线![]() 上的所有点均在直线
上的所有点均在直线![]() 的下方,
的下方,
∴对![]() ,有
,有![]() 恒成立,
恒成立,
即![]() (其中
(其中![]() )恒成立,
)恒成立,
∴![]() .
.
又![]() ,∴解得
,∴解得![]() ,
,
∴实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目