题目内容
10. 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,E为棱PC的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,E为棱PC的中点.(1)PA∥平面BDE;
(2)证明:PA⊥BD.
分析 (1)连结AC,BD,交于点O,连结OE,则OE∥AP,由此能证明PA∥平面BDE.
(2)因为∠DAB=60°,AB=2AD,由余弦定理得BD=$\sqrt{3}$AD,利用勾股定理证明BD⊥AD,根据PD⊥底面ABCD,易证BD⊥PD,根据线面垂直的判定定理和性质定理,可证PA⊥BD;
解答 解:(1)证明:连结AC,BD,交于点O,
∵四边形ABCD为平行四边形,∴O是AC中点,
∵E是PC中点,∴OE∥AP,
又AP?平面BDE,OE?平面BDE,
∴PA∥平面BDE.
(2)证明:因为∠DAB=60°,AB=2AD,由余弦定理得BD=$\sqrt{3}$AD,
从而BD2+AD2=AB2,故BD⊥AD,
又PD⊥底面ABCD,可得BD⊥PD,
所以BD⊥平面PAD.故PA⊥BD.
点评 本题主要考查线面垂直的性质定理和判定定理,以及点到面的距离,考查了同学们观察、推理以及创造性地分析问题、解决问题能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生
表2:女生
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)从表二中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
参考数据与公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
临界值表:
表1:男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
(2)从表二中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
| 男生 | 女生 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
临界值表:
| P(K2>k0) | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
7.已知m、n是两条不同的直线,α、β是两个不同的平面,则下列命题正确的是( )
| A. | 若m∥n,m∥α且n∥β,则α∥β?????????? | |
| B. | 若m⊥n,m∥α且n∥β,则α⊥β? | |
| C. | 若m∥α且n⊥m,则n⊥α???????????????????? | |
| D. | 若m⊥n,m⊥α且n⊥β,则α⊥β |
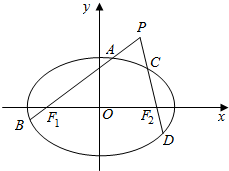 如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.
如图,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左右焦点分别为F1,F2,离心率为$\frac{{\sqrt{2}}}{2}$,它的四个顶点连成的菱形的面积为8$\sqrt{2}$.过动点P(不在x轴上)的直线PF1,PF2与椭圆的交点分别为A,B和C,D.