题目内容
12.设集合A={x|f(x)=x2-x-2,且f(x)<0},B={x|x2-(2m+1)x+2m<0}.(Ⅰ)化简集合A;
(Ⅱ)若A∩B=B,求实数m的取值范围.
分析 (Ⅰ)把A中f(x)解析式代入f(x)<0,求出解集即可确定出A;
(Ⅱ)根据A与B的交集为B,得到B为A的子集,表示出B中不等式的解集,根据2m与1的大小,分类讨论求出m的范围即可.
解答 解:(Ⅰ)根据A得:x2-x-2<0,即(x-2)(x+1)<0,
解得:-1<x<2,
则A=(-1,2);
(Ⅱ)∵A∩B=B,∴B⊆A,
由B中不等式变形得:(x-2m)(x-1)<0,
(1)当2m>1,即m>$\frac{1}{2}$时,解得:1<x<2m,即B=(1,2m),
可得2m≤2,即m≤1,
此时m的范围为$\frac{1}{2}$<m≤1;
(2)当2m=1,即m=$\frac{1}{2}$时,B=∅,满足题意;
(3)当2m<1,即m<$\frac{1}{2}$时,解得:2m<x<1,即B=(2m,1),
可得2m≥-1,即m≥-$\frac{1}{2}$,
此时m的范围为-$\frac{1}{2}$≤m<$\frac{1}{2}$,
综上,m的范围为[-$\frac{1}{2}$,1].
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
3.已知a,b,c,d成等比数列,且曲线y=x2-2x+3的顶点坐标为(b,c),则a+d=( )
| A. | 3 | B. | $\frac{9}{2}$ | C. | $\frac{5}{2}$ | D. | 4 |
20.某公司招聘来8名员工,平均分配给下属的甲、乙两个部门,其中两名英语翻译人员不能分在同一个部门,则不同的分配方案共有( )
| A. | 10种 | B. | 20种 | C. | 40种 | D. | 80种 |
7.如图,四边形ABCD中,$\overrightarrow{AB}$=$\overrightarrow{DC}$,则必有( )
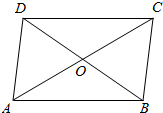

| A. | $\overrightarrow{AD}$=$\overrightarrow{CB}$ | B. | $\overrightarrow{OA}$=$\overrightarrow{OC}$ | C. | $\overrightarrow{AC}$=$\overrightarrow{DB}$ | D. | $\overrightarrow{DO}$=$\overrightarrow{OB}$ |
4.函数f(x)=x3+3x2+3ax-4既有极大值又有极小值,则函数g(x)=x+$\frac{a}{x}$-2a在区间(1,+∞)上一定( )
| A. | 有最小值 | B. | 有最大值 | C. | 是减函数 | D. | 是增函数 |
1.下列命题正确的是( )
| A. | 若两条直线和同一个平面所成的角相等,则这两条直线平行 | |
| B. | 若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行 | |
| C. | 三角形的两条边平行于一个平面,则第三边也平行于这个平面 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行 |
2.不等式|3x+6|≤21的解集是( )
| A. | ∅ | B. | [-9,5] | C. | (-∞,-9)∪(5,+∞) | D. | R |