题目内容
17.已知函数f(x)=4x+$\frac{a}{x}$+b(a,b∈R)为奇函数.(Ⅰ)若f(1)=5,求函数f(x)的解析式;
(Ⅱ)当a=-2时,对任意x∈[1,4]上,函数y=f(x)的图象在函数y=t的图象的下方,求实数t的范围.
分析 (Ⅰ)利用奇函数的定义求出b,利用f(1)=5,求出a,即可求函数f(x)的解析式;
(Ⅱ)当a=-2时,f(x)=4x-$\frac{2}{x}$,x∈[1,4],函数单调递增,求出函数的最大值,即可求实数t的范围.
解答 解:(Ⅰ)∵函数f(x)=4x+$\frac{a}{x}$+b(a,b∈R)为奇函数,
∴f(-x)=-f(x),即-4x-$\frac{a}{x}$+b=-4x-$\frac{a}{x}$-b,
∴b=0,
∵f(1)=5,
∴4+a=5,
∴a=1,
∴f(x)=4x+$\frac{1}{x}$;
(Ⅱ)当a=-2时,f(x)=4x-$\frac{2}{x}$,x∈[1,4],函数单调递增,
∴f(x)∈[2,$\frac{31}{2}$],
∵对任意x∈[1,4]上,函数y=f(x)的图象在函数y=t的图象的下方,
∴t>$\frac{31}{2}$.
点评 本题考查函数的解析式,考查函数的奇偶性、单调性,确定函数的解析式是关键.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
8.已知点O是△ABC的外接圆圆心,且AB=3,AC=4.若存在非零实数x、y,使得$\overrightarrow{AO}=x\overrightarrow{AB}+y\overrightarrow{AC}$,且x+2y=1,则cos∠BAC的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{2}}}{3}$ | D. | $\frac{1}{3}$ |
9.点M为圆P内不同于圆心的定点,过点M作圆Q与圆P相切,则圆心Q的轨迹是( )
| A. | 圆 | B. | 椭圆 | C. | 圆或线段 | D. | 线段 |
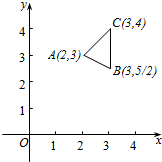 已知点(x,y)在△ABC所包围的阴影区域内(包含边界),若B是使得z=ax-y取得最大值的最优解,则实数a的取值范围为[-$\frac{1}{2}$,+∞).
已知点(x,y)在△ABC所包围的阴影区域内(包含边界),若B是使得z=ax-y取得最大值的最优解,则实数a的取值范围为[-$\frac{1}{2}$,+∞). 如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.
如图,四棱锥P-ABCD的底面为正方形,PA⊥底面ABCD,E、F分别为AB、PD的中点.