题目内容
16．设a＞0，a≠1，函数f（x）=loga$\frac{x-2}{x+2}$-loga（x-1）-1有且仅有两个零点，求a的取值范围．分析 先求出f（x）的定义域，再令f（x）=0，得出方程ax2+（a-1）x-2a+2=0，
由f（x）有且仅有两个零点，得该方程在f（x）的定义域内有两个不相等的实数根，
利用二次函数的图象与性质列出不等式组，即可求出a的取值范围．
解答 解：根据题意得$\left\{\begin{array}{l}{\frac{x-2}{x+2}＞0}\\{x-1＞0}\end{array}\right.$，
解得x＞2；
∴f（x）的定义域为（2，+∞）；
又f（x）=loga$\frac{x-2}{x+2}$-loga（x-1）-1=loga$\frac{x-2}{（x+2）（x-1）}$-1，
令loga$\frac{x-2}{（x+2）（x-1）}$-1=0，
得loga$\frac{x-2}{（x+2）（x-1）}$=1，
即$\frac{x-2}{（x+2）（x-1）}$=a，
化简得ax2+（a-1）x-2a+2=0；
∵f（x）有且仅有两个零点，
∴方程ax2+（a-1）x-2a+2=0在（2，+∞）上有两个不相等的实数根；
设g（x）=ax2+（a-1）x-2a+2，如图所示：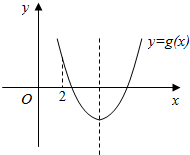
则$\left\{\begin{array}{l}{a＞0且a≠1}\\{△{=（a-1）}^{2}-4a（-2a+2）＞0}\\{-\frac{a-1}{2a}＞2}\\{g（2）=4a+2（a-1）-2a+2＞0}\end{array}\right.$；
解得0＜a＜$\frac{1}{9}$．
点评 本题考查了对数函数的图象与性质的应用问题，也考查了二次函数的图象与性质的应用问题，考查了转化思想的应用问题，是综合性题目．
练习册系列答案
相关题目
6．已知变量x服从正态分布N（4，σ2），且P（x＞2）=0.6，则P（x＞6）=（ ）
| A． | 0.4 | B． | 0.3 | C． | 0.2 | D． | 0.1 |
7．等差数列{an}的前项和为Sn，已知am+1+am-1-am2=0，S2m-1=38，则m=（ ）
| A． | 5 | B． | 6 | C． | 8 | D． | 10 |
11．已知集合A={x|x2+x＞2}，B={-1，0，1，2}，则（∁RA）∩B等于（ ）
| A． | {-1，0，1} | B． | {1，2} | C． | {-1，0} | D． | {2} |
阅读下面的两个程序：
5．函数y=4sinx，x∈[-π，π]的单调性是（ ）
| A． | 在[-π，0]上是增函数，在[0，π]上是减函数 | |
| B． | 在[-$\frac{π}{2}$，$\frac{π}{2}$]上是增函数，在[-π，-$\frac{π}{2}$]和[$\frac{π}{2}$，π]上都是减函数 | |
| C． | 在[0，π]上是增函数，在[-π，0]上是减函数 | |
| D． | 在[$\frac{π}{2}$，π]和[-π，-$\frac{π}{2}$]上是增函数，在[-$\frac{π}{2}$，$\frac{π}{2}$]上是减函数 |