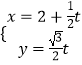题目内容
【题目】在直角坐标系中xOy中，已知曲线E经过点P（1， 
），其参数方程为 
（α为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系．
（1）求曲线E的极坐标方程；
（2）若直线l交E于点A、B，且OA⊥OB，求证： 
为定值，并求出这个定值．
【答案】
（1）解：将点P（1， 
），代入曲线E的方程： 
，
解得a2=3，
所以曲线E的普通方程为 
=1，
极坐标方程为 
=1
（2）解：不妨设点A，B的极坐标分别为A（ρ1，θ），B（ρ2， 
），
则代入曲线E的极坐标方程，可得 
= 
= 
，
即 
为定值
【解析】（1）将点P（1， ），代入曲线E的方程，求出a2=3，可得曲线E的普通方程，即可求曲线E的极坐标方程；（2）利用点的极坐标，代入极坐标方程，化简，即可证明结论．
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
目标测试系列答案
【题目】调查表明：甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性，现将这三项的指标分别记为x，y，z，并对它们进行量化：0表示不合格，1表示临界合格，2表示合格，再用综合指标ω=x+y+z的值评定这种农作物的长势等级，若ω≥4，则长势为一级；若2≤ω≤3，则长势为二级；若0≤ω≤1，则长势为三级，为了了解目前这种农作物长势情况，研究人员随机抽取10块种植地，得到如表中结果：
种植地编号 | A1 | A2 | A3 | A4 | A5 |
（x，y，z） | （1，1，2） | （2，1，1） | （2，2，2） | （0，0，1） | （1，2，1） |
种植地编号 | A6 | A7 | A8 | A9 | A10 |
（x，y，z） | （1，1，2） | （1，1，1） | （1，2，2） | （1，2，1） | （1，1，1） |
（Ⅰ）在这10块该农作物的种植地中任取两块地，求这两块地的空气湿度的指标z相同的概率；
（Ⅱ）从长势等级是一级的种植地中任取一块地，其综合指标为A，从长势等级不是一级的种植地中任取一块地，其综合指标为B，记随机变量X=A﹣B，求X的分布列及其数学期望．
