题目内容
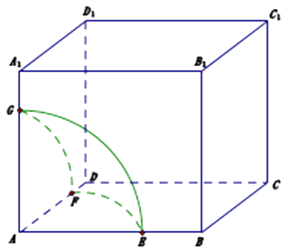
【题目】如图1,菱形ABCD的边长为12,∠BAD=60°,AC与BD交于O点.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M是棱BC的中点,DM=6 ![]() .
. 
(I)求证:平面ODM⊥平面ABC;
(II)求二面角M﹣AD﹣C的余弦值.
【答案】证明:(Ⅰ)∵ABCD是菱形,
∴AD=DC,OD⊥AC,
△ADC中,AD=DC=12,∠ADC=120°,
∴OD=6,
又M是BC中点,∴ ![]() ,
,
∵OD2+OM2=MD2,∴DO⊥OM,
∵OM,AC面ABC,OM∩AC=O,
∴OD⊥面ABC,
又∵OD平面ODM,∴平面ODM⊥平面ABC.…
(Ⅱ)解:由题意,OD⊥OC,OB⊥OC,
又由(Ⅰ)知OB⊥OD,建立如图所示空间直角坐标系,
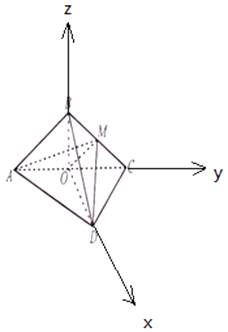
由条件知: ![]()
故 ![]() ,
,
设平面MAD的法向量 ![]() ,
,
则 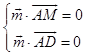 ,即
,即 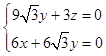 ,令
,令 ![]() ,则x=3,z=9
,则x=3,z=9
∴ ![]()
由条件知OB⊥平面ACD,故取平面ACD的法向量为 ![]()
所以, 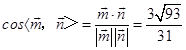
由图知二面角M﹣AD﹣C为锐二面角,
故二面角M﹣AD﹣C的余弦值为 ![]() .
.
【解析】(Ⅰ)推导出OD⊥AC,DO⊥OM,从而OD⊥面ABC,由此能证明平面ODM⊥平面ABC.(Ⅱ)由OD⊥OC,OB⊥OC,OB⊥OD,建立空间直角坐标系,利用向量法能求出二面角M﹣AD﹣C的余弦值.
【考点精析】根据题目的已知条件,利用平面与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目