题目内容
【题目】如图,在棱长为1的正方体ABCD﹣A1B1C1D1中,动点P在其表面上运动,且|PA|=x,把点的轨迹长度L=f(x)称为“喇叭花”函数,给出下列结论: ① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]()
其中正确的结论是: . (填上你认为所有正确的结论序号)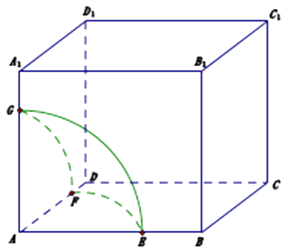
【答案】②③④
【解析】解:∵动点P在其表面上运动,且|PA|=x,
∴点的轨迹是以A为球心,PA为半径的球的球面与正方体的面的交线,①当0<x≤1时,点的轨迹如图(1),则f(x)=3× ![]() ,所以
,所以 ![]() ,故①错;
,故①错;
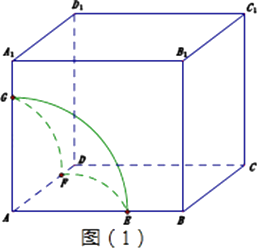
②当1 ![]() 时,点P的轨迹在六个面都有,
时,点P的轨迹在六个面都有,
x= ![]() 时,在与A相邻的三个面上的圆弧的圆心角为
时,在与A相邻的三个面上的圆弧的圆心角为 ![]() ,在另外三个面上都是四分之一圆弧,
,在另外三个面上都是四分之一圆弧,
∴ ![]() =
= ![]() ,故③正确③当x=
,故③正确③当x= ![]() 时,如图(3)点P的轨迹是三段相等圆弧,圆弧的长是四分之一个圆,半径是1,
时,如图(3)点P的轨迹是三段相等圆弧,圆弧的长是四分之一个圆,半径是1,
∴这条轨迹的长度是:3× ![]() ,故②正确;
,故②正确;
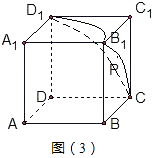
④当 ![]() 时,点P的轨迹是三段相等圆弧,在与点A不相邻的三个面上,圆弧半径R=
时,点P的轨迹是三段相等圆弧,在与点A不相邻的三个面上,圆弧半径R= ![]() ,
,
圆弧的圆心角为 ![]() ,∴f
,∴f ![]() ,故④正确;
,故④正确;
所以答案是:②③④
【考点精析】通过灵活运用棱柱的结构特征,掌握两底面是对应边平行的全等多边形;侧面、对角面都是平行四边形;侧棱平行且相等;平行于底面的截面是与底面全等的多边形即可以解答此题.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目


