题目内容
20.已知函数f(x)=(ax2+2x-2)ex,其中e是自然对数的底数,a∈R.(1)若a=1,求曲线f(x)在点(1,f(1))处的切线方程;
(2)若a<0,求f(x)的单调区间;
(3)若a=-2,函数f(x)的图象与函数$g(x)=\frac{1}{3}{x^3}+\frac{1}{2}{x^2}+m$的图象有3个不同的交点,求实数m的取值范围.
分析 (1)求出导数,求得切线的斜率和切点,由点斜式方程,可得切线的方程;
(2)求出导数,对a讨论,a=-1,-1<a<0,a<-1,解不等式,即可得到所求单调区间;
(3)由题意可得f(x)-g(x)的图象与x轴有3个不同的交点,即y=m与$y=(-2{x^2}+2x-2){e^x}-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}$的图象有3个不同的交点,
令$F(x)=(-2{x^2}+2x-2){e^x}-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}$,求出导数,求得单调区间和极值,只要令m介于两极值之间.
解答 解:(1)函数f(x)=(x2+2x-2)ex,的导数为f′(x)=x(x+4)ex,
曲线f(x)在点(1,f(1))处的切线斜率为5e,切点为(1,e),
即有切线方程为y-e=5e(x-1),即为切线5ex-y-4e=0;
(2)$f'(x)=ax(x+\frac{2a+2}{a}){e^x}$,
因为a<0,所以a=-1时,f'(x)≤0恒成立,f(x)在(-∞,+∞)上递减;
-1<a<0时,f(x)在(-∞,0)和$(-\frac{2a+2}{a},+∞)$上递减,在$(0,-\frac{2a+2}{a})$上递增;
a<-1时,f(x)在$(-∞,-\frac{2a+2}{a})$和(0,+∞)上递减,在$(-\frac{2a+2}{a},0)$上递增;
综上,a=-1时,f(x)的减区间为R;
-1<a<0时,f(x)的增区间为$(0,-\frac{2a+2}{a})$,减区间为(-∞,0)和$(-\frac{2a+2}{a},+∞)$;
a<-1时,f(x)的增区间为$(-\frac{2a+2}{a},0)$,减区间为$(-∞,-\frac{2a+2}{a})$和(0,+∞);
(3)a=-2时,可得$f(x)-g(x)=(-2{x^2}+2x-2){e^x}-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}-m$,
原问题等价于f(x)-g(x)的图象与x轴有3个不同的交点,
即y=m与$y=(-2{x^2}+2x-2){e^x}-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}$的图象有3个不同的交点,
令$F(x)=(-2{x^2}+2x-2){e^x}-\frac{1}{3}{x^3}-\frac{1}{2}{x^2}$,
F'(x)=-x(x+1)(2ex+1),
令F'(x)=0,x=0或x=-1,
x∈(-∞,-1)∪(0,+∞),F'(x)<0,F(x)在(-∞,-1)和(0,+∞)上递减;
x∈(-1,0),F'(x)>0,F(x)在和(-1,0)上递增;
所以F(x)在x=-1时去的极小值$F(-1)=-\frac{6}{e}-\frac{1}{6}$,F(x)在x=0时取得极大值F(0)=-2,
所以$m∈(-\frac{6}{e}-\frac{1}{6},-2)$.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查分类讨论的思想方法和函数方程的转化思想,考查运算能力,属于中档题.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
| A. | $\sqrt{5}$ | B. | $\sqrt{29}$ | C. | $3\sqrt{2}$ | D. | 4 |
| A. | p是假命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | B. | p是假命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 | ||
| C. | p是真命题,¬p:?x∈(0,$\frac{π}{2}$),f(x)≥0 | D. | p是真命题,¬p:?x0∈(0,$\frac{π}{2}$),f(x)≥0 |
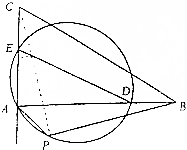 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.