题目内容

10．三角函数f（x）=cos2x+2sinx的最小正周期为（　　）
A．$\frac{π}{2}$B．πC．2πD．4π

分析 分别求得y=cos2x和 y=2sinx的最小正周期，再取周期的最小公倍数，即为它的周期．

解答 解：函数 y=cos2x的最小正周期为$\frac{2π}{2}$=π，而函数y=2sinx的最小正周期为2π，
故函数f（x）=cos2x+2sinx的最小正周期为2π，
故选：C．

点评 本题主要考查两角差的余弦公式，余弦函数的周期性，属于基础题．

练习册系列答案
相关题目
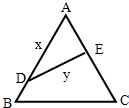20．如图，某公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
（Ⅰ）设AD=x，DE=y，求y关于x的函数关系式；
（Ⅱ）如果DE是灌溉水管，我们希望它最短，则DE的位置应在哪里？请予以证明．
1．已知集合M={x|（1-x）x＞0}，N={y|y=x2+2x+3}，则（∁RM）∩N=（　　）
A．{x|0＜x＜1}B．{x|x＞1}C．{x|x≥2}D．{x|1＜x＜2}
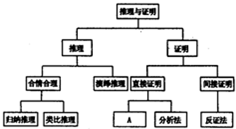18．如图是教材选修1-2中《推理与证明》一章的知识结构图，请把A处填入适当的方法综合法．
5．化简求值：（$\frac{a}{a-b}$-$\frac{{a}^{2}}{{a}^{2}-2ab+{b}^{2}}$）÷（$\frac{a}{a+b}$-$\frac{{a}^{2}}{{a}^{2}-{b}^{2}}$），其中a=2，b=-3．
15．设x，y满足约束条件$\left\{\begin{array}{l}{2x-3y+6≥0}\\{x-1≤y}\\{x≥0}\\{y≥0}\end{array}\right.$，若目标函数z=ax+by（a＞0，b＞0）的最大值为8，则$\frac{2}{a}$+$\frac{4}{b}$的最小值为$\frac{49}{4}$．
2．定义在R上的函数f（x）满足：f（x）=$\frac{{2}^{x}}{f（x-4）}$，则$\frac{f（16）}{f（0）}$=256．
19．在平面直角坐标系中，O为坐标原点，A（1，0），B（0，3），C（3，0），动点D满足|CD|=1，则|$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OD}$|的最小值是4．
20．已知函数f（x）=（ax2+2x-2）ex，其中e是自然对数的底数，a∈R．
（1）若a=1，求曲线f（x）在点（1，f（1））处的切线方程；
（2）若a＜0，求f（x）的单调区间；
（3）若a=-2，函数f（x）的图象与函数$g（x）=\frac{1}{3}{x^3}+\frac{1}{2}{x^2}+m$的图象有3个不同的交点，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网