题目内容
10.已知f(x)=log${\;}_{\frac{1}{2}}$[a2x-3(ab)x+2b2x+1],其中1+lgb=1ga,求使f(x)<0的x的取值范围.分析 若f(x)<0,则a2x-3(ab)x+2b2x>0,分解后可得(ax-bx)(ax-2bx)>0,结合1+lgb=1ga即a=10b,在两边各除b2x后,可得[(10)x-1][(10)x-2]>0,结合指数函数的图象和性质,可得答案.
解答 解:∵1+lgb=1ga,
∴a=10b>0,
∴f(x)=log${\;}_{\frac{1}{2}}$[a2x-3(ab)x+2b2x+1]=log${\;}_{\frac{1}{2}}$[(ax-bx)(ax-2bx)+1]
若f(x)<0,则(ax-bx)(ax-2bx)+1>1,
即(ax-bx)(ax-2bx)>0,
即[(10)x-1][(10)x-2]>0,
即(10)x<1,或(10)x>2,
即x<0,或x>lg2.
点评 本题考查的知识点是对数函数的图象和性质,指数函数的图象和性质,对数的运算性质,指数的运算性质,十字相乘法,综合性可,转化困难,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.函数f(x)=loga(2-x)-1(a>0,且a≠1)的图象恒过定点 ( )
| A. | (1,0) | B. | (0,-1) | C. | (1,1) | D. | (1,-1) |
20.已知f(lnx)=x2,则f($\frac{1}{2}$)=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{e}$ | D. | e |
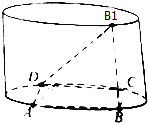 如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)
如图,圆柱底面直径为10,母线BB1=6,矩形ABCD内接于圆柱的下底面,BC=6,求直线DB1与BC所成角的大小.(结果用反三角函教值表示)