题目内容
9.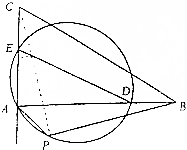 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
分析 连结PD,PE,PC,利用圆周角定理结合已知及三角形全等的判定定理,可得△PBD≌△PCE,进而∠PBA=∠PCA,从而得到A、P、B、C四点共圆.
解答 证明:如图所示,连结PD,PE,PC,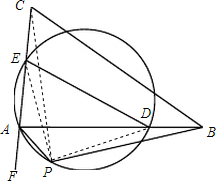
∵四边形APED是圆内接四边形,
∴∠PAD=∠PED,∠PAF=∠PDE,
又∵AP为∠BAC的外角平分线,
∴∠PAD=∠PAF,
∴∠PED=∠PDE,
∴PD=PE,
又∵∠ADP=∠AEP,
∴∠BDP=∠CEP,
又∵BD=CE,
∴△PBD≌△PCE,
即∠PBA=∠PCA,
即A、P、B、C四点共圆.
点评 本题考查的知识点是四点共圆,其中添加辅助线,得到全等三角形,是解答的关键.

练习册系列答案
相关题目