题目内容
某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:


 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.
问:(1)求这40辆小型车辆车速的众数和中位数的估计值.(2)若从车速在 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
(1)众数的估计值等于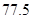 .中位数的估计值为:
.中位数的估计值为: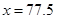 ;
;
(2) 的分布列为:
的分布列为:
均值
0 1 2 
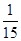
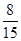
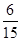
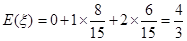 .
.
解析试题分析:(1)众数的估计值为最高的矩形的中点;如下图,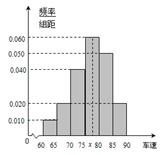
设图中虚线所对应的车速为 ,若
,若 两侧的矩形的面积相等,则这个
两侧的矩形的面积相等,则这个 就是中位数的估计值;
就是中位数的估计值;
(2)首先看随机变量可以取哪些值?从图中可知,这40辆车中,车速在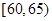 的车辆数为:
的车辆数为: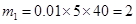 辆,车速在
辆,车速在 的车辆数为:
的车辆数为: 辆.所以
辆.所以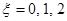 .显然这是一个超几何分布,由此可得其分布列及期望.
.显然这是一个超几何分布,由此可得其分布列及期望.
试题解析:(1)众数的估计值为最高的矩形的中点,即众数的估计值等于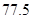 (2分)
(2分)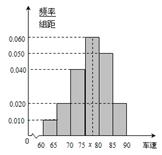
设图中虚线所对应的车速为 ,则中位数的估计值为:
,则中位数的估计值为: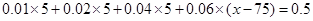 ,解得
,解得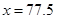
即中位数的估计值为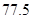 (5分)
(5分)
(2)从图中可知,车速在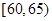 的车辆数为:
的车辆数为: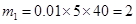 (辆),
(辆),
车速在 的车辆数为:
的车辆数为: (辆) (7分)
(辆) (7分)
∴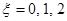 ,
,  ,
,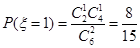 ,
,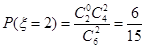 ,
, 的分布列为:
的分布列为:
(10分)
0 1 2 
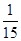
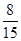
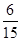
均值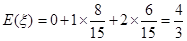 . (12分
. (12分
考点:1、统计基础知识;2、随机变量的分布列及期望3、超几何分布.

 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附:

2013年4月14日,CCTV财经频道报道了某地建筑市场存在违规使用未经淡化海砂的现象.为了研究使用淡化海砂与混凝土耐久性是否达标有关,某大学实验室随机抽取了60个样本,得到了相关数据如下表:
| | 混凝土耐久性达标 | 混凝土耐久性不达标 | 总计 |
| 使用淡化海砂 | 25 |  | 30 |
| 使用未经淡化海砂 | 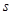 | 15 | 30 |
| 总计 | 40 | 20 | 60 |
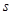 ,
, 的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?
的值,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为使用淡化海砂与混凝土耐久性是否达标有关?(Ⅱ)若用分层抽样的方法在使用淡化海砂的样本中抽取了6个,现从这6个样本中任取2个,则取出的2个样本混凝土耐久性都达标的概率是多少?
参考数据:
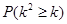 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
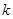 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
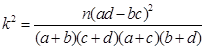
 (年)与所支出的维修费
(年)与所支出的维修费 (万元)的数据资料,算得
(万元)的数据资料,算得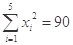 ,
, ,
, ,
,  .
.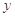 对使用年限
对使用年限 的线性回归方程
的线性回归方程 ;
; ,
, ,其中
,其中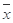 ,
, 为
为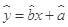 .
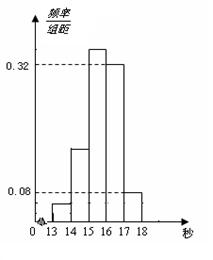
.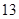 秒与
秒与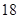 秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组
秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组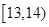 ,第二组
,第二组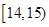 ,…,第五组
,…,第五组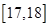 ,下图是按上述分组方法得到的频率分布直方图.
,下图是按上述分组方法得到的频率分布直方图.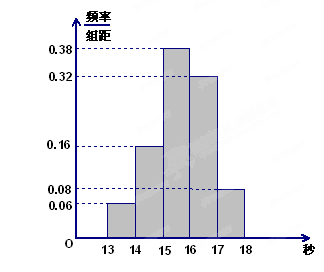

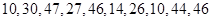

 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的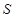 大小为多少?并说明
大小为多少?并说明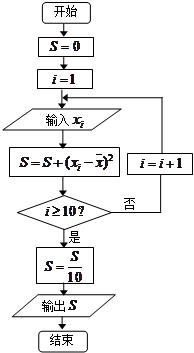

 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在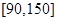 范围为及格);
范围为及格);