题目内容
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
附:

(1)能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系;(2)概率是 .
.
解析试题分析:本题考查生活中的实际问题、独立性检验问题以及随机事件的概率,考查运用概率知识解决实际问题的能力,考查学生的分析能力和计算能力.第一问,通过分析题意,列出列联表,填出表中所有数据,利用 某学校餐厅新推出A,B,C,D四款套餐,某一天四款套餐销售情况的条形图如下. 为了了解同学对新推出的四款套餐的评价,对每位同学都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示: 某学校的三个学生社团的人数分布如下表(每名学生只能参加一个社团): 已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表: 公式计算出数值,与
公式计算出数值,与 作比较,判断出概率值,从而确定学生常吃零食与患龋齿是否有关系;第二问,先列出4个人收集数据与处理数据的所有情况,再从中挑出符合题意的情况,从而求出概率.
作比较,判断出概率值,从而确定学生常吃零食与患龋齿是否有关系;第二问,先列出4个人收集数据与处理数据的所有情况,再从中挑出符合题意的情况,从而求出概率.
试题解析:(1)由题意可得列联表:
因为 不常吃零食 常吃零食 总计 不患龋齿 60 100 160 患龋齿 140 500 640 总计 200 600 800  。
。
所以能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系.
(2)设其他工作人员为丙和丁,4人分组的所有情况如下表小组 1 2 3 4 5 6 收集数据 甲乙 甲丙 甲丁 乙丙 乙丁 丙丁 处理数据 丙丁 
滴水穿石初中暑假快乐提升晨光出版社系列答案
暑假作业本浙江教育出版社系列答案
学习与探究暑假学习系列答案
名校假期作业西安出版社系列答案
新路学业快乐假期暑假作业新疆青少年出版社系列答案
暑假作业及活动新疆美术摄影出版社系列答案
快乐暑假假日乐园广西师范大学出版社系列答案
暑假作业黄山书社系列答案
暑假快乐假期新疆青少年出版社系列答案
新坐标暑假作业青海人民出版社系列答案
满意
一般
不满意
A套餐
50%
25%
25%
B套餐
80%
0
20%
C套餐
50%
50%
0
D套餐
40%
20%
40%

(Ⅰ)若同学甲选择的是A款套餐,求甲的调查问卷被选中的概率;
(Ⅱ)若想从调查问卷被选中且填写不满意的同学中再选出2人进行面谈,求这两人中至少有一人选择的是D款套餐的概率.
学校要对这三个社团的活动效果进行抽样调查,按分层抽样的方法从三个社团成员中抽取18人,结果拳击社被抽出了6人.
围棋社
舞蹈社
拳击社
男生
5
10
28
女生
15
30
m
(Ⅰ)求拳击社女生有多少人;
(Ⅱ)从围棋社指定的3名男生和2名女生中随机选出2人参加围棋比赛,求这两名同学是一名男生和一名女生的概率.
若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示数学成绩与地理成绩,例如:表中数学成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18.
A
B
C
A
7
20
5
B
9
18
6
C
a
4
b
(1)若在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩为C等级的学生中,已知a≥10,b≥8,求数学成绩为A等级的人数比C等级的人数少的概率.


 名学生被考官L面试,求
名学生被考官L面试,求 是指大气中直径小于或等于
是指大气中直径小于或等于 微米的颗粒物,也称为可吸入肺颗粒物.我国
微米的颗粒物,也称为可吸入肺颗粒物.我国 微克/立方米以下空气质量为一级;在
微克/立方米以下空气质量为一级;在 微克/立方米之间空气质量为二级;在
微克/立方米之间空气质量为二级;在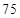 微克/立方米以上空气质量为超标.某试点城市环保局从该市市区
微克/立方米以上空气质量为超标.某试点城市环保局从该市市区 年上半年每天的
年上半年每天的 天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
天的数据作为样本,监测值如下图茎叶图所示(十位为茎,个位为叶).
 天数据,记
天数据,记 表示抽到
表示抽到 天计算)中平均有多少天的空气质量达到一级或二级.
天计算)中平均有多少天的空气质量达到一级或二级.


 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.
 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).