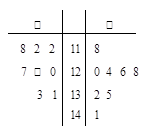题目内容
在每年的春节后,某市政府都会发动公务员参与到植树活动中去.为保证树苗的质量,该市林管部门在植树前,都会在植树前对树苗进行检测.现从甲乙两种树苗中各抽测了10株树苗的高度,量出树苗的高度如下(单位:厘米):
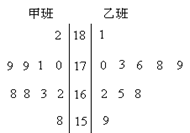
甲:
乙: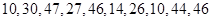
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两种树苗的高度作比较,写出两个统计结论;
(2)设抽测的10株甲种树苗高度平均值为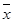 ,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的
,将这10株树苗的高度依次输入按程序框图进行的运算,问输出的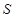 大小为多少?并说明
大小为多少?并说明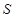 的统计学意义.
的统计学意义.
(1)茎叶图: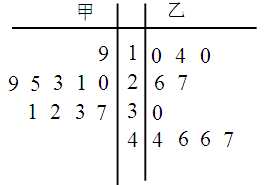
统计结论:
①.甲种树苗的平均高度小于乙种树苗的平均高度;
②.甲种树苗比乙种树苗长得更整齐;
③.甲种树苗的中位数为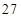 ,乙种树苗的中位数为
,乙种树苗的中位数为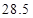 ;
;
④.甲种树苗的高度基本上是对称的,而且大多数集中在均值附近,乙种树苗的高度分布较为分散.
(在以上结论中,写两个即可)
(2)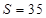 ,
,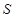 表示
表示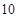 株甲树苗高度的方差,是描述树苗高度离散程度的量.
株甲树苗高度的方差,是描述树苗高度离散程度的量.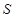 值越小,表示长得越整齐,
值越小,表示长得越整齐,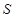 值越大,表示长得越参差不齐.
值越大,表示长得越参差不齐.
解析试题分析:(1)本题中,茎叶图的茎表示十位上的数字(题中已给出),叶表示个位上的数字,故将甲乙两种树苗的高度的个位数字填在两边相应位置上.统计结论从平均数、方差、中位数、众数入手,分析树苗的平均高度及集中度.
(2)从框图可以看出,该程序是求树苗高度的方差,所以首先求出甲树苗的高度的平均值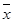 ,然后求出方差
,然后求出方差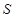 .
.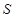 是描述树苗高度离散程度的量.
是描述树苗高度离散程度的量.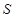 值越小,表示长得越整齐,
值越小,表示长得越整齐,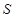 值越大,表示长得越参差不齐.
值越大,表示长得越参差不齐.
试题解析:(1)茎叶图:
统计结论:
①.甲种树苗的平均高度小于乙种树苗的平均高度;
②.甲种树苗比乙种树苗长得更整齐;
③.甲种树苗的中位数为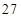 ,乙种树苗的中位数为
,乙种树苗的中位数为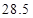 ;
;
④.甲种树苗的高度基本上是对称的,而且大多数集中在均值附近,乙种树苗的高度分布较为分散.
(在以上结论中,每个结论2分,但总分不超过4分)
(2) 8分
8分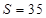 10分
10分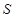 表示
表示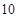 株甲树苗高度的方差,是描述树苗高度离散程度的量.
株甲树苗高度的方差,是描述树苗高度离散程度的量.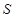 值越小,表示长得越整齐,
值越小,表示长得越整齐,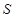 值越大,表示长得越参差不齐. 12分
值越大,表示长得越参差不齐. 12分
考点:统计及样本数据的基本数字特征.

 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:
 | A | B | C |
| A | 7 | 20 | 5 |
| B | 9 | 18 | 6 |
| C | a | 4 | b |
(1)若在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩为C等级的学生中,已知a≥10,b≥8,求数学成绩为A等级的人数比C等级的人数少的概率.

 名学生被考官L面试,求
名学生被考官L面试,求


 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.
 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).
 ,求甲通过初赛的概率.
,求甲通过初赛的概率.