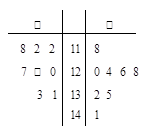题目内容
某数学老师对本校2013届高三学生某次联考的数学成绩进行分析,按1:50进行分层抽样抽取的20名学生的成绩进行分析,分数用茎叶图记录如下: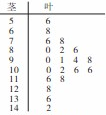
得到频率分步表如下:
(1)求表中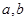 的值,并估计这次考试全校学生数学成绩及格率(分数在
的值,并估计这次考试全校学生数学成绩及格率(分数在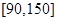 范围为及格);
范围为及格);
(2)从大于等于110分的学生中随机选2名学生得分,求2名学生的平均得分大于等于130分的概率.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:本题主要考查茎叶图的读法和频率分布表中数据的计算.考查学生的分析能力和计算能力.第一问,结合频率分布表和茎叶图,利用频率=频数÷样本总数来计算;第二问,分别数出所有符合题意的种数,再求概率.
试题解析:(Ⅰ)由茎叶图可知分数在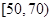 范围内的有2人,在
范围内的有2人,在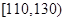 范围内的有3人,
范围内的有3人,
∴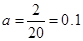 ,
,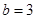 . 4分
. 4分
从茎叶图可知分数在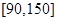 范围内的有13人,
范围内的有13人,
所以估计全校数学成绩及格率为 . 6分
. 6分
(Ⅱ)设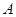 表示事件“大于等于110分的学生中随机选2名学生得分,平均得分大于等于130分”,
表示事件“大于等于110分的学生中随机选2名学生得分,平均得分大于等于130分”,
由茎叶图可知大于等于110分有5人,记这5人分别为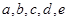 , 7分
, 7分
则选取学生的所有可能结果为: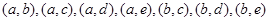
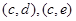 ,
,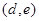 ,基本事件数为10, 9分
,基本事件数为10, 9分
事件“2名学生的平均得分大于等于130分” ,也就是“这两个学生的分数之和大于等于260”,
所以可能结果为:(118,142),(128,136),(128,142),(136,142),
共4种情况,基本事件数为4, 11分
所以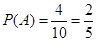 . 12分
. 12分
考点:1.茎叶图;2.频率;3.随机事件的概率.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案


 后得到如图4的频率分布直方图.
后得到如图4的频率分布直方图.
 的车辆中任抽取2辆,求抽出的2辆车中车速在
的车辆中任抽取2辆,求抽出的2辆车中车速在 的车辆数
的车辆数 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).


 ,求
,求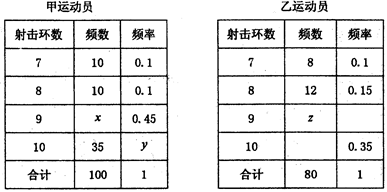
 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求