题目内容
【题目】已知函数![]()
![]() 在区间
在区间![]() 上的最大值为9,最小值为1,记
上的最大值为9,最小值为1,记![]() ;
;
(1)求实数![]()
![]() 的值;
的值;
(2)若不等式![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,其中
,其中![]()
![]()
![]()
![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,如果存在一个常数
个小区间,如果存在一个常数![]() ,使得和式
,使得和式![]() 恒成立,则称函数
恒成立,则称函数![]() 为在
为在![]() 上的有界变差函数,试判断函数
上的有界变差函数,试判断函数![]() 是否为在
是否为在![]() 上的有界变差函数?若是,求
上的有界变差函数?若是,求![]() 的最小值;若不是,请说明理由.
的最小值;若不是,请说明理由.
【答案】(1)![]() ,
,![]() ;(3)
;(3)![]() 或
或![]() ;(3)是,
;(3)是,![]() .
.
【解析】
(1)根据![]() 在
在![]() 上的单调性可得
上的单调性可得![]() 的最大值和最小值,结合已知条件可求
的最大值和最小值,结合已知条件可求![]() 的值.
的值.
(2)不等式![]() 等价于
等价于![]() ,由后者可以得到
,由后者可以得到![]() ,从而可求
,从而可求![]() 的取值范围.
的取值范围.
(3)对任意的![]() 上的划分,必定存在
上的划分,必定存在![]() ,使得
,使得![]() ,从而可得
,从而可得![]() ,故可得
,故可得![]() 的最大值,从而可判断
的最大值,从而可判断![]() 是
是![]() 上的有界变差函数且
上的有界变差函数且![]() .
.
(1)因为![]() 的对称轴为直线
的对称轴为直线![]() ,
,![]()
故![]() 在
在![]() 为增函数,所以
为增函数,所以![]() ,
,
![]() ,解得
,解得![]() ,又
,又![]() ,解得
,解得![]() .
.
所以![]() .
.
(2)由(1)得![]() ,
,
因为![]() ,所以
,所以![]() 等价于
等价于![]() ,
,
所以![]() ,故
,故![]() 或
或![]() ,解得
,解得![]() 或
或![]() .
.
(3)当![]() 时,
时,![]() ,此时
,此时![]() ,
,
且![]() 在
在![]() 为减函数,在
为减函数,在![]() 为增函数.
为增函数.
设![]()
![]()
![]()
![]() 将区间
将区间![]() 任意划分成
任意划分成![]() 个小区间,
个小区间,
且![]() ,则存在
,则存在![]() ,
,
使得![]() ,
,
所以![]()
![]() ,
,
整理得到![]() ,
,
因为![]() ,
,![]() ,
,
故![]() ,当且仅当
,当且仅当![]() 即
即![]() 时等号成立,
时等号成立,
故![]() 是
是![]() 上的有界变差函数,又
上的有界变差函数,又![]() ,所以
,所以![]() .
.

【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类蔬菜.过去50周的资料显示,该地周光照量![]() (小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量
(小时)都在30小时以上,其中不足50小时的周数有5周,不低于50小时且不超过70小时的周数有35周,超过70小时的周数有10周.根据统计,该基地的西红柿增加量![]() (百斤)与使用某种液体肥料
(百斤)与使用某种液体肥料![]() (千克)之间对应数据为如图所示的折线图.
(千克)之间对应数据为如图所示的折线图.

(1)依据数据的折线图,是否可用线性回归模型拟合![]() 与
与![]() 的关系?请计算相关系数
的关系?请计算相关系数![]() 并加以说明(精确到0.01).(若
并加以说明(精确到0.01).(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
(2)蔬菜大棚对光照要求较大,某光照控制仪商家为该基地提供了部分光照控制仪,但每周光照控制仪最多可运行台数受周光照量![]() 限制,并有如下关系:
限制,并有如下关系:
周光照量 |
|
|
|
光照控制仪最多可运行台数 | 3 | 2 | 1 |
若某台光照控制仪运行,则该台光照控制仪周利润为3000元;若某台光照控制仪未运行,则该台光照控制仪周亏损1000元.若商家安装了3台光照控制仪,求商家在过去50周周总利润的平均值.
附:相关系数公式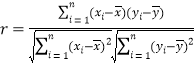 ,参考数据
,参考数据![]() ,
,![]() .
.