��Ŀ����
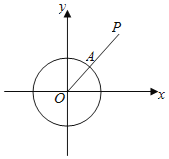
����Ŀ����ƽ��ֱ������ϵxOy�У����ڡ�O��x2+y2��1��˵��P������ϵ������һ�㣬��P����O�ľ���SP�Ķ������£���P��O�غϣ�SP��r����P����O�غϣ�����OP���O�Ľ���ΪA��SP��AP�ij��ȣ���ͼ����
��1��ֱ��2x+2y+1��0��Բ�ڲ��ֵĵ㵽��O�������Ϊ_____��
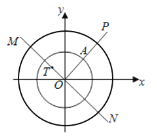
��2�����߶�MN�ϴ��ڵ�T��ʹ�ã�
�ٵ�T�ڡ�O�ڣ�
����P���߶�MN������ST��SP���������߶�MN�����Ϊ_____��
���𰸡�1![]() 4
4
��������
��1��������Ӧ��ͼ����ͼ���֪��ֱ����2x+2y+1��0��ֱʱ��Ӧ�Ľ���P����ʱP����O�ľ���������ý⣻
��2�������ɵ�SP��1����˵��߶�MN��ԭ��ʱ�����߶�MN��ԭ��ʱ��MN�����Ϊ4�����ý�.
������Ӧ��ͼ����ͼ��
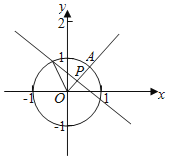
��ͼ���֪��ֱ����2x+2y+1��0��ֱʱ��Ӧ�Ľ���P��![]() ȡ����Сֵ����ʱP����O�ľ������
ȡ����Сֵ����ʱP����O�ľ������
��ʱOP![]() ����AP��1��OP��1
����AP��1��OP��1![]() ��
��
��2������T����O�ڣ���ST��1��
��ST��SP��������SP��1��
��P���߶�MN����P��Բ�ڣ�������SP��1��
��P��Բ�⣬P��������ԭ��ΪԲ�ģ�2Ϊ�뾶��Բ���ڲ������߽磩
�����߶�MN��ԭ��ʱ��MN�����Ϊ1+2+1��4��

 ��ѧʵ����ϵ�д�
��ѧʵ����ϵ�д�����Ŀ���й��人��2019��10��18����2019��10��27�ճɹ��ٰ��˵��߽���������˶���.����109�����ҵ�9300�����˶�Ա̨ͬ����.�������ҵĽ��𣬽��ư��ǰ3�����£�
���� | ���� | ���� | ͭ�� | �������� |
�й� | 133 | 64 | 42 | 239 |
����˹ | 51 | 53 | 57 | 161 |
���� | 21 | 31 | 36 | 88 |
ij��ѧ�����߲��÷ֲ�����ķ�ʽ�����й��Ͱ�����ý���ѡ���г�ȡ��22������.����22���������ȡ3�ˣ� ����3�����й�ѡ��ǡ��1�˵ĸ���Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
����Ŀ�����绥������������й�������ÿ�����㽭ʡ������ͩ������ٰ�������Ի�����ʢ�ᣬ���ּ�ڴ�й������绥����ͨ�Ĺ���ƽ̨���ʻ������������ε��й�ƽ̨���ø�������������ʶ�ڹ�ʶ��ı�����ں����д���Ӯ.2019��10��20����22�գ����������绥����������ھ��У�Ϊ�˴��˳���ٿ�����ί������ļ��1 000��־Ը��.ij����Ϊ���˽�־Ը�ߵĻ������������������100��־Ը�ߵ����䣬�õ��������������λ��Ϊ34�꣬������![]() ���ڵ�����Ϊ15�������ݵ�����������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ:
���ڵ�����Ϊ15�������ݵ�����������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ:

��1����![]() ��
��![]() ��ֵ�������־Ը�ߵ�ƽ�����䣨ͬһ��������ø���������е�ֵ��������
��ֵ�������־Ը�ߵ�ƽ�����䣨ͬһ��������ø���������е�ֵ��������
��2����δ��־Ը����Ҫͨ���ֳ������͵�¼���������������ֳ����������ַ�ʽ��������.��100λ־Ը�ߵı�����ʽ�����������±���ʾ����������ı���ͨ������˵����
���ڷ�����ĸ��ʲ�����0.001��ǰ���£���Ϊ��ѡ�����ֱ�����ʽ���Ա��й�ϵ��?
���� | Ů�� | �ܼ� | |
�ֳ����� | 50 | ||
���籨�� | 31 | ||
�ܼ� | 50 |
�ο���ʽ������: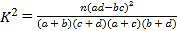 ������
������![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |

