Question

【题目】已知动直线：与轴交于点，过点作直线，交轴于点，点满足，的轨迹为.

（1）求的方程；

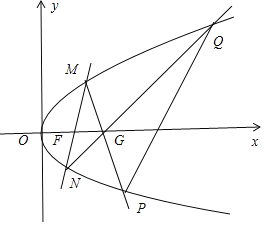
（2）已知点，点，过作斜率为的直线交于，两点，延长，分别交于，两点，记直线的斜率为，求证：为定值.

Answer 1

【答案】（1） （2）证明见解析

【解析】

（1）动直线与轴交于点．由直线，可得直线的方程为：，交轴于点，．设，点满足，代入即可得出轨迹方程．

（2）设，，，的坐标依次为，，2，3，．直线的方程为：，与抛物线方程联立化为：，设直线的方程为：，与抛物线方程联立化为：，利用根与系数的关系、斜率计算公式即可得出．

解：（1）将代入得，∴，

∵，∴可设：，将代入得，∴.

设，则，，

由，得，即，

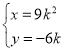∴的方程为.

（2）设，，，，直线的方程为，

由，消去得，∴，，

设的方程为，由，消去得，

∴，即，同理，

由已知得，，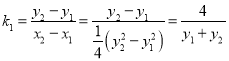

∴，

∵，∴为定值.