题目内容
【题目】已知函数
.
（1）若不等式
的解集为
，求实数
的值；
（2）在（1）的条件下，若存在实数
使
成立，求实数
的取值范围.
【答案】（1）
（2）
【解析】【试题分析】（1）借助绝对值的几何意义求出不等式的解集，再与已知解集进行比对建立方程进行求解；（2）先依据题设条件构造函数φ(n)＝f(n)＋f(－n)，然后将问题进行等价转化为求函数φ(n)＝f(n)＋f(－n)的最小值求解：
解 (1)由|2x－a|＋a≤6得|2x－a|≤6－a，
∴a－6≤2x－a≤6－a，即a－3≤x≤3，∴a－3＝－2，
∴
.
(2)由(1)知f(x)＝|2x－1|＋1.
令φ(n)＝f(n)＋f(－n)，
则φ(n)＝|2n－1|＋|2n＋1|＋2＝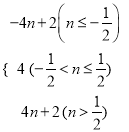
∴φ(n)的最小值为4，故实数m的取值范围是[4，＋∞)．
练习册系列答案
相关题目
【题目】某城市理论预测2000年到2004年人口总数与年份的关系如下表所示
年份200x（年） | 0 | 1 | 2 | 3 | 4 |
人口数y（十）万 | 5 | 7 | 8 | 11 | 19 |
（1）请画出上表数据的散点图；
（2）请根据上表提供的数据，求出Y关于x的线性回归方程Y=bx+a；
（3）据此估计2005年该城市人口总数．
