Question

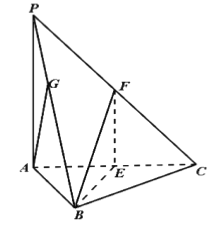
【题目】如图，在三棱锥中，底面是边长为4的正三角形，底面，点分别为的中点，且异面直线和所成的角的大小为.

（1）求证：平面平面；

（2）求三棱锥的体积.

Answer 1

【答案】（1）证明过程详见解析（2）

【解析】

（1）由，为的中点，证得，再由线面垂直的性质，得到，利用线面垂直的判定定理，得到平面，进而证得平面平面；

（2）取的中点，连结，得到底面，且异面直线和所成的角的大小为，即，进而利用棱锥的体积公式，即可求解。

（1）证明：∵，为的中点，

∴

又平面，平面，

∴

∵

∴平面，

∵平面

∴平面平面

（2）解：：取的中点，连结

∵三角形为正三角形，底面

∴，又∵分别为的中点

∴，，

又∵异面直线和所成的角的大小为

∴

∴三角形为正三角形，

∴

又∵，∴

∴

又∵

∴三棱锥的体积.