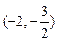题目内容
(本小题满分15分)已知函数 ,若函数
,若函数 的图象与函数
的图象与函数 的图象关于原点对称.(1)写出函数
的图象关于原点对称.(1)写出函数 的解析式;(2)求不等式
的解析式;(2)求不等式 的解集
的解集 ; (3)问是否存在
; (3)问是否存在 ,使不等式
,使不等式 的解集恰好是
的解集恰好是 ?若存在,请求出
?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 ,若函数
,若函数 的图象与函数
的图象与函数 的图象关于原点对称.(1)写出函数
的图象关于原点对称.(1)写出函数 的解析式;(2)求不等式
的解析式;(2)求不等式 的解集
的解集 ; (3)问是否存在
; (3)问是否存在 ,使不等式
,使不等式 的解集恰好是
的解集恰好是 ?若存在,请求出
?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(1) (2)
(2) (3)
(3)
 (2)
(2) (3)
(3)
(1)设 为
为 图象上任意一点,
图象上任意一点,
则 关于原点的对称点
关于原点的对称点 在
在 的图象上,
的图象上,
所以 ,即
,即
(2)由 ,原不等式可化为
,原不等式可化为
∵ ∴
∴ ,且
,且
 即
即
(3)假设存在 使命题成立,则
使命题成立,则
由 ,得
,得 
∵ ,∴不等式组
,∴不等式组 的解集恰为
的解集恰为 ,只需不等式
,只需不等式 ,即
,即 的解集为
的解集为 ,且
,且 ,
,
易得 即为所求, 故存在实数
即为所求, 故存在实数 使命题成立。
使命题成立。
 为
为 图象上任意一点,
图象上任意一点,则
 关于原点的对称点
关于原点的对称点 在
在 的图象上,
的图象上,所以
 ,即
,即
(2)由
 ,原不等式可化为
,原不等式可化为
∵
 ∴
∴ ,且
,且
 即
即
(3)假设存在
 使命题成立,则
使命题成立,则 由
 ,得
,得 
∵
 ,∴不等式组
,∴不等式组 的解集恰为
的解集恰为 ,只需不等式
,只需不等式 ,即
,即 的解集为
的解集为 ,且
,且 ,
,易得
 即为所求, 故存在实数
即为所求, 故存在实数 使命题成立。
使命题成立。
练习册系列答案
相关题目
 在
在 处连续,试确定a的值
处连续,试确定a的值 ,在区间
,在区间 上画出函数
上画出函数 的图像。
的图像。
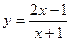 按
按 平移使其化简为反比例函数表达式,则
平移使其化简为反比例函数表达式,则



 在
在 平面上沿曲线运动,速度大小不 变,其在
平面上沿曲线运动,速度大小不 变,其在 轴
轴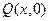 的运动速度
的运动速度 的图象大致为 ( )
的图象大致为 ( )
 的反函数是
的反函数是  与
与 在同一直角坐标系下的图像是如图中的( )
在同一直角坐标系下的图像是如图中的( )
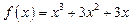 的图象按向量
的图象按向量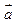 平移后得到函数
平移后得到函数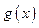 的图象,若函数
的图象,若函数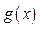 满足
满足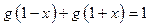 ,则向量
,则向量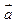 的坐标是( )
的坐标是( )