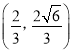题目内容
【题目】已知椭圆![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,且
,且![]() 与抛物线
与抛物线![]() 的焦点重合.
的焦点重合.
(1)求椭圆的标准方程;
(2)若过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,过
两点,过![]() 的直线交椭圆于
的直线交椭圆于![]() 两点,且
两点,且![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)椭圆的标准方程为![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]() .
.
【解析】试题分析:(1)由题可知)抛物线![]() 的焦点为
的焦点为![]() ,所以
,所以![]() ,然后根据离心率可得a值,从而得出椭圆标准方程(2)根据题意则需求出AC和BD的长度表达式,显然可以根据直线与椭圆的弦长公式求得,所以设
,然后根据离心率可得a值,从而得出椭圆标准方程(2)根据题意则需求出AC和BD的长度表达式,显然可以根据直线与椭圆的弦长公式求得,所以设![]() ,
, ![]() ,直线
,直线![]() 的方程为
的方程为![]() ,代入椭圆方程
,代入椭圆方程![]() ,
, ![]() ,同理求出AC的长度,然后化简即得
,同理求出AC的长度,然后化简即得![]()
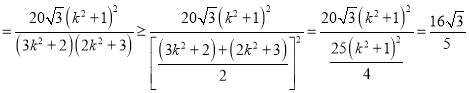 .
.
解析:
(1)抛物线![]() 的焦点为
的焦点为![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以![]() ,所以椭圆的标准方程为
,所以椭圆的标准方程为![]() .
.
(2)(i)当直线![]() 的斜率
的斜率![]() 存在且
存在且![]() 时,
时,
直线![]() 的方程为
的方程为![]() ,代入椭圆方程
,代入椭圆方程![]() ,
,
并化简得![]() .
.
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
![]()
![]() .
.
易知![]() 的斜率为
的斜率为![]() ,
,
所以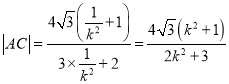 .
.
![]()
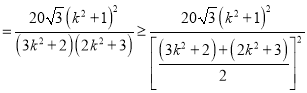
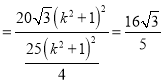 .
.
当![]() ,即
,即![]() 时,上式取等号,故
时,上式取等号,故![]() 的最小值为
的最小值为![]() .
.
(ii)当直线![]() 的斜率不存在或等于零时,易得
的斜率不存在或等于零时,易得![]() .
.
综上, ![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目