题目内容
【题目】已知二次函数f(x)=ax2﹣4x+c的值域为[0,+∞).
(1)判断此函数的奇偶性,并说明理由;
(2)判断此函数在[ ![]() ,+∞)的单调性,并用单调性的定义证明你的结论;
,+∞)的单调性,并用单调性的定义证明你的结论;
(3)求出f(x)在[1,+∞)上的最小值g(a),并求g(a)的值域.
【答案】
(1)解:由二次函数f(x)=ax2﹣4x+c的值域为[0,+∞),得a>0且 ![]() ,
,
解得ac=4.
∵f(1)=a+c﹣4,f(﹣1)=a+c+4,a>0且c>0,从而f(﹣1)≠f(1),f(﹣1)≠﹣f(1),
∴此函数是非奇非偶函数
(2)解:函数的单调递增区间是[ ![]() ,+∞).设x1、x2是满足
,+∞).设x1、x2是满足 ![]() 的任意两个数,从而有
的任意两个数,从而有 ![]() ,∴
,∴ ![]() .又a>0,∴
.又a>0,∴ ![]() ,
,
从而 ![]() ,
,
即 ![]() ,从而f(x2)>f(x1),∴函数在[
,从而f(x2)>f(x1),∴函数在[ ![]() ,+∞)上是单调递增
,+∞)上是单调递增
(3)解:f(x)=ax2﹣4x+c,又a>0, ![]() ,x∈[1,+∞)
,x∈[1,+∞)
当 ![]() ,即0<a≤2时,最小值g(a)=f(x0)=0
,即0<a≤2时,最小值g(a)=f(x0)=0
当 ![]() ,即a>2时,最小值
,即a>2时,最小值 ![]()
综上,最小值 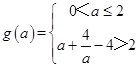
当0<a≤2时,最小值g(a)=0
当a>2时,最小值 ![]()
综上y=g(a)的值域为[0,+∞)
【解析】(1)由二次函数f(x)=ax2﹣4x+c的值域,推出ac=4,判断f(﹣1)≠f(1),f(﹣1)≠﹣f(1),得到此函数是非奇非偶函数.(2)求出函数的单调递增区间.设x1、x2是满足 ![]() 的任意两个数,列出不等式,推出f(x2)>f(x1),即可判断函数是单调递增.(3)f(x)=ax2﹣4x+c,当
的任意两个数,列出不等式,推出f(x2)>f(x1),即可判断函数是单调递增.(3)f(x)=ax2﹣4x+c,当 ![]() ,即0<a≤2时,当
,即0<a≤2时,当 ![]() ,即a>2时求出最小值即可.
,即a>2时求出最小值即可.
【考点精析】通过灵活运用二次函数的性质,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目